
����Ŀ����֪����ͼ����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��t��s����������и����⣺ 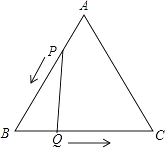
��1�����ABC�������
��2����tΪ��ֵ�ǣ���PBQ��ֱ�������Σ�
��3��̽�����Ƿ����ijһʱ��t��ʹ�ı���APQC������ǡ�ABC����İ˷�֮�壿������ڣ����t��ֵ����������˵�����ɣ�
���𰸡�
��1���⣺��ͼ������A��AD��BC�����BAC=30�㣬
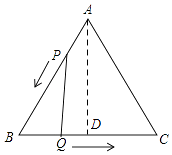
��AC=4��
��CD= ![]() AC=2��
AC=2��
��Rt��ACD��AD= ![]() =2
=2 ![]() ��
��
���ABC�����= ![]() ��BC��AD=
��BC��AD= ![]() ��4��2
��4��2 ![]() =4
=4 ![]()
��2���⣺�辭��t�룬��PBQ��ֱ�������Σ���AP=tcm��BQ=tcm��
��ABC�У�AB=BC=4cm����B=60�㣬
��BP=��4��t��cm��
����PBQ��ֱ�������Σ�������������
�� ����BQP=90��ʱ��BQ= ![]() BP��
BP��
��t= ![]() ��4��t����
��4��t����
���t= ![]() ���룩��
���룩��
�ڵ���BPQ=90��ʱ��BP= ![]() BQ��
BQ��
4��t= ![]() t��
t��
���t= ![]() ���룩��
���룩��
������������t= ![]() ���
��� ![]() ��ʱ����PBQ��ֱ��������
��ʱ����PBQ��ֱ��������
��3���⣺������������t��
���ɣ���ͼ����QD��AB��D�����BQD=30�㣬

��QD= ![]() BD=
BD= ![]() ��
�� ![]() t=
t= ![]() t��
t��
���BQP�����= ![]() ��BP��QD
��BP��QD
= ![]() ����4��t����
����4��t���� ![]() t
t
= ![]() t��
t�� ![]() t2��
t2��
���ı���APQC������ǡ�ABC����� ![]() ʱ����BQP������ǡ�ABC�����
ʱ����BQP������ǡ�ABC����� ![]() ��
��
�� ![]() t��
t�� ![]() t2=
t2= ![]() ��4
��4 ![]() ��
��
����ã�t2��4t+6=0��
�ߡ�=b2��4ac=16��4��1��6=��8��0��
�����������t��ʹ�ı���APQC������ǡ�ABC����İ˷�֮�壮
����������1������A��AD��BC�����ݹ��ɶ������AD�ij������������ε������ʽ���н�ɣ���2������������������ۣ��١�BPQ=90�㣻�ڡ�BQP=90�㣬Ȼ����ֱ��������BQP�и���BP��BQ�ij��͡�B�Ķ���������⼴�ɣ���3������QD��AB��D�����ݡ�BQD=30�㣬�õ�QD= ![]() BD=
BD= ![]() ��
�� ![]() t=
t= ![]() t��Ȼ������ı���APQC������ǡ�ABC����İ˷�֮�壬�ɵó�һ������t�ķ��̣���������⣬��˵��������������tֵ����������н⣬��ô�����tֵ���ɣ�
t��Ȼ������ı���APQC������ǡ�ABC����İ˷�֮�壬�ɵó�һ������t�ķ��̣���������⣬��˵��������������tֵ����������н⣬��ô�����tֵ���ɣ�
�����㾫����ͨ��������������ʽ�ͺ�30�Ƚǵ�ֱ�������Σ����ո����б�ʽ��=b2-4ac��������Է�Ϊ3�������1������>0ʱ��һԪ���η�����2������ȵ�ʵ����2������=0ʱ��һԪ���η�����2����ͬ��ʵ����3������<0ʱ��һԪ���η���û��ʵ��������ֱ���������У����һ����ǵ���30�㣬��ô�����Ե�ֱ�DZߵ���б�ߵ�һ�뼴���Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��BC��OA����B=��A=100�㣬�Իش��������⣺
��1����ͼ1��ʾ����֤��OB��AC�� 
��2����ͼ2������E��F��BC�ϣ��������FOC=��AOC������OEƽ�֡�BOF�������EOC�Ķ����� 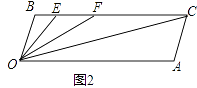
��3���ڣ�2���������£���ƽ���ƶ�AC����ͼ3�����OCB����OFB��ֵ�� �� 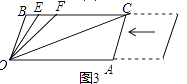
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����ͼ1��AB��CD����PAB=130�㣬��PCD=120�㣬���APC�Ķ����� С����˼·�ǣ���P��PE��AB��ͨ��ƽ�������������APC��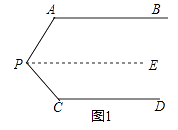
��1����С����˼·������á�APC�Ķ���Ϊ�ȣ�
��2������Ǩ�ƣ���ͼ2��AB��CD����P������OM���˶����ǡ�PAB=������PCD=�£�����P��B��D����֮���˶�ʱ���ʡ�APC�������֮���к�������ϵ����˵�����ɣ� 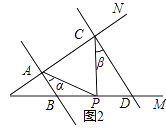
��3���ڣ�2���������£������P��B��D��������˶�ʱ����P���O��B��D���㲻�غϣ�����ֱ��д����APC�������֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����̣�x-1����x+3��=12��Ϊax2+bx+c=0����ʽ��a��b��c��ֵΪ��������
A.1��2��-15
B.1��-2��-15
C.-1��-2��-15
D.-1��2��-15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ƚϴ�С������ֵ�����_____�����������Ƚϴ�С������ֵ���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��a��0����B��0��b�����㣨a��4��2+|b��6|=0���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��B��C��A��O��·���ƶ��� 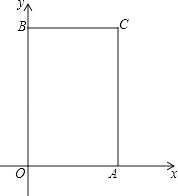
��1��д��A��B��C��������ꣻ
��2������P�ƶ���6��ʱ�������ʱP���λ�ã���д����P��λ�ã�
��3�����ᣨ2����B��P���㣬���߶�BP����ƽ��h����λ��h��0�����õ�B��P�䣬��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣���h��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� 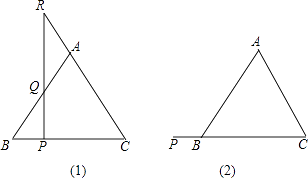
��1��P�ǵ���������ABC�ױ�BC�ϵ�һ�����㣬����P��BC�Ĵ��ߣ���AB�ڵ�Q����CA���ӳ����ڵ�R����۲�AR��AQ�������кι�ϵ����֤����IJ��룮
��2�������P���ŵױ�BC���ڵ�ֱ�ߣ�����C��B�ķ����˶���CB���ӳ�����ʱ����1�������õĽ��ۻ�������������ͼ��2�������ͼ�Σ�������֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com