
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图1所示,求证:OB∥AC; 
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数; 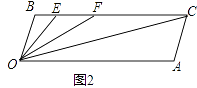
(3)在(2)的条件下,若平行移动AC,如图3,则∠OCB:∠OFB的值是 . 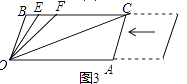
【答案】
(1)解:∵BC∥OA,
∴∠B+∠O=180°,
∵∠A=∠B
∴∠A+∠O=180°,
∴OB∥AC
(2)解:∵∠A=∠B=100°,由(1)得∠BOA=180°﹣∠B=80°,
∵∠FOC=∠AOC,并且OE平分∠BOF,
∴∠EOF= ![]() ∠BOF,∠FOC=
∠BOF,∠FOC= ![]() ∠FOA,
∠FOA,
∴∠EOC=∠EOF+∠FOC= ![]() (∠BOF+∠FOA)=
(∠BOF+∠FOA)= ![]() ∠BOA=40°
∠BOA=40°
(3)1:2
【解析】解: (3)结论:∠OCB:∠OFB的值不发生变化. 理由为:
∵BC∥OA,
∴∠FCO=∠COA,
又∵∠FOC=∠AOC,
∴∠FOC=∠FCO,
∴∠OFB=∠FOC+∠FCO=2∠OCB,
∴∠OCB:∠OFB=1:2.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握平移的性质(①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】某体育运动学校准备在甲、已两位射箭选手中选出成绩比较稳定的一人参加集训,两人各射击了5箭,已知他们的总成绩(单位:环)相同,如下表所示: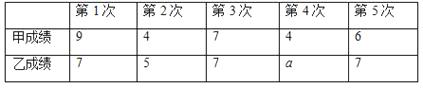
(1)试求出表中a的值;
(2)请你通过计算,从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一季度的利润是82.75万元,其中一月份的利润是25万元,若利润平均每月的增长率为x , 则依题意列方程为( )
A.25(1+x)2=82.75
B.25+50x=82.75
C.25+25(1+x)2=82.75
D.25[1+(1+x)+(1+x)2]=82.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙丙丁四支足球队在全国甲级联赛中进球数分别为:9,9,x , 7,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )
A.10
B.9
C.8
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).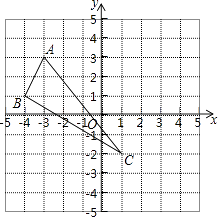
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′( , ); B′( , );
C′( , ).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB, 小明说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,
可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连接GF,则GF一定平行于AB.”
他们四人中,有个人的说法是正确的.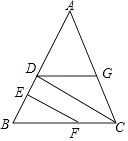
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是边长为4cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: 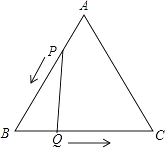
(1)求△ABC的面积;
(2)当t为何值是,△PBQ是直角三角形?
(3)探究:是否存在某一时刻t,使四边形APQC的面积是△ABC面积的八分之五?如果存在,求出t的值;不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com