
【题目】甲乙丙丁四支足球队在全国甲级联赛中进球数分别为:9,9,x , 7,若这组数据的众数与平均数恰好相等,则这组数据的中位数是( )
A.10
B.9
C.8
D.7
【答案】B
【解析】解答:∵这组数据的众数与平均数恰好相等,∴9+9+x+7=9×4,∴x=11,又这组数据共有4个,∴中位数是按从小到大排列后的第2与第3个的平均数即 ![]() ,所以选B.
,所以选B.
分析:求中位数时一定要先拍好顺序,然后再根据数据个数的奇偶来确定中位数,如果数据有奇数个,则中间的数字即为所求,如果是偶数个则中间两个数的平均数是中位数.
【考点精析】关于本题考查的算术平均数和中位数、众数,需要了解总数量÷总份数=平均数.解题关键是根据已知条件确定总数量以及与它相对应的总份数;中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某厂一月份的总产量为500吨,三月份的总产量达到为720吨.若平均每月增长率是x , 则可以列方程( )
A.500(1+2x)=720
B.500(1+x)2=720
C.500(1+x2)=720
D.720(1+x)2=500
查看答案和解析>>
科目:初中数学 来源: 题型:
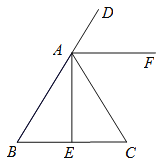
【题目】如图,在△ABC中,AB=AC,AE是高,AF是△ABC外角∠CAD的平分线.
(1)用尺规作图:作∠AEC的平分线EN(保留作图痕迹,不写作法和证明);
(2)设EN与AF交于点M,判断△AEM的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题不一定成立的是( )
A.斜边与一条直角边对应成比例的两个直角三角形相似;
B.两个等腰直角三角形相似;
C.两边对应成比例且有一个角相等的两个三角形相似;
D.各有一个角等于95°的两个等腰三角形相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
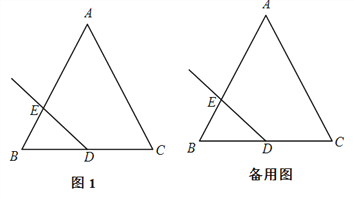
【题目】在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.
(1)依题意将图1补全;
(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;
想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;
想法3:由等腰三角形三线合一,可得AD是∠BAC的角平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF…….
请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);
(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题:
(1)如图1所示,求证:OB∥AC; 
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.试求∠EOC的度数; 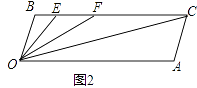
(3)在(2)的条件下,若平行移动AC,如图3,则∠OCB:∠OFB的值是 . 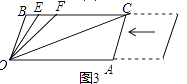
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com