
【题目】如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题: 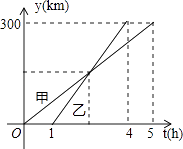
(1)A,B两城相距千米;
(2)若两车同时出发,乙车将比甲车早到小时;
(3)乙车的速度为千米/时;乙车出发后小时两车相遇;
(4)直接写出,当乙车出发几小时,甲、乙两车相距40千米.
【答案】
(1)300
(2)2
(3)100;1.5
(4)解:设甲车对应的函数解析式为y=kx,
5k=300,得k=60,
∴甲车对应的函数解析式为y=60x,
设乙车对应的函数解析式为y=ax+b,
![]() ,得
,得 ![]() ,
,
即乙车对应的函数解析式为y=100x﹣100,
∴|(100x﹣100)﹣60x|=40,
解得, ![]() ,
,
当x= ![]() 时,乙出发
时,乙出发 ![]() 小时,
小时,
当x= ![]() 时,乙出发
时,乙出发 ![]() 小时,
小时,
即当乙车出发 ![]() 小时或
小时或 ![]() 小时时,甲、乙两车相距40千米
小时时,甲、乙两车相距40千米
【解析】解:(1)由图象可得, A,B两城相距300千米,
所以答案是:300;
2)由图象可得,
若两车同时出发,乙车将比甲车早到:5﹣(4﹣1)=5﹣3=2(小时),
所以答案是:2;
3)由图象可得,
乙车的速度为:300÷(4﹣1)=100千米/时,
设乙车出发x小时时两车相遇,![]() ,
,
解得,x=1.5,
所以答案是:100,1.5;


 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数. 小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.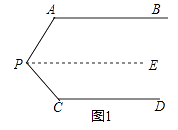
(1)按小明的思路,易求得∠APC的度数为度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由; 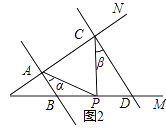
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足(a﹣4)2+|b﹣6|=0,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O﹣B﹣C﹣A﹣O的路线移动. 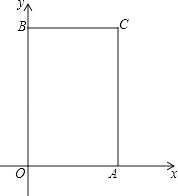
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图: 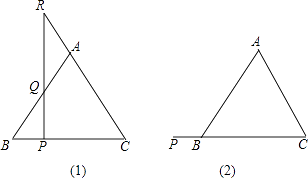
(1)P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.
(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com