
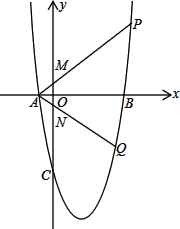
【题目】如图1,在平面直角坐标系中,抛物线y=x2-4x-5与x轴分别交于A、B(A在B的左边),与y轴交于点C,直线AP与y轴正半轴交于点M,交抛物线于点P,直线AQ与y轴负半轴交于点N,交抛物线于点Q,且OM=ON,过P、Q作直线l
(1) 探究与猜想:
① 取点M(0,1),直接写出直线l的解析式
取点M(0,2),直接写出直线l的解析式
② 猜想:
我们猜想直线l的解析式y=kx+b中,k总为定值,定值k为__________,请取M的纵坐标为n,验证你的猜想
(2) 如图2,连接BP、BQ.若△ABP的面积等于△ABQ的面积的3倍,试求出直线l的解析式
【答案】(1)①PQ:y=6x-29,PQ:y=6x-26;
(2)k=6;
(3)直线PQ的解析式为y=6x-21
【解析】试题分析:(1)、①、首先根据二次函数解析式得出点A的坐标,然后根据待定系数法求出直线l的解析式;②、设设M(0,n),然后分别求出直线AP和AQ的解析式,然后根据直线与抛物线的交点求出点P和点Q的坐标,从而得出直线PQ的解析式,得出k的值;(2)、根据三角形的面积关系得出点P的坐标,从而得出直线PQ的函数解析式.
试题解析:(1) ① P(6,7)、Q(4,-5),PQ:y=6x-29
② 设M(0,n) AP的解析式为y=nx+n AQ的解析式为y=-nx-n
联立![]() ,整理得x2-(4+n)x-(5+n)=0
,整理得x2-(4+n)x-(5+n)=0
∴xA+xP=-1+xP=4+n,xP=5+n 同理:xQ=5-n
设直线PQ的解析式为y=kx+b
联立![]() ,整理得x2-(4+k)x-(5+b)=0 ∴xP+xQ=4+k
,整理得x2-(4+k)x-(5+b)=0 ∴xP+xQ=4+k
∴5+n+5-n=4+k,k=6
(3) ∵S△ABP=3S△ABQ ∴yP=-3yQ ∴kxP+b=-3(kxQ+b) ∵k=6 ∴6xP+18xQ=-b
∴6(5+n)+18(5-n)=4b,解得b=3n-30
∵xP·xQ=-(5+b)=-5-3n+30=(5+n)(5-n),解得n=3 ∴P(8,27)
∴直线PQ的解析式为y=6x-21


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】我区很多学校开展了大课间活动.某校初三(1)班抽查了10名同学每分钟仰卧起坐的次数,数据如下(单位:次):51,69,64,52,64,72,48,52,76,52,那么这组数据的众数与中位数分别为( ).
A.64和58
B.58和64
C.58和52
D.52和58
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).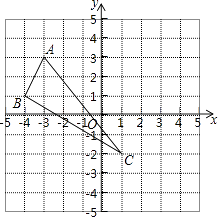
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′( , ); B′( , );
C′( , ).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC的两边OA,OC分别在x轴,y轴的正半轴上,且点B(4,3),反比例函数y=![]() 图象与BC交于点D,与AB交于点E,其中D(1,3).
图象与BC交于点D,与AB交于点E,其中D(1,3).
(1)求反比例函数的解析式及E点的坐标;
(2)求直线DE的解析式;
(3)若矩形OABC对角线的交点为F (2,![]() ),作FG⊥x轴交直线DE于点G.
),作FG⊥x轴交直线DE于点G.
①请判断点F是否在此反比例函数y=![]() 的图象上,并说明理由;
的图象上,并说明理由;
②求FG的长度.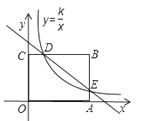
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小刚、小颖一起研究一道数学题,如图,已知EF⊥AB,CD⊥AB, 小明说:“如果还知道∠CDG=∠BFE,则能得到∠AGD=∠ACB.”
小亮说:“把小明的已知和结论倒过来,即由∠AGD=∠ACB,
可得到∠CDG=∠BFE.”
小刚说:“∠AGD一定大于∠BFE.”
小颖说:“如果连接GF,则GF一定平行于AB.”
他们四人中,有个人的说法是正确的.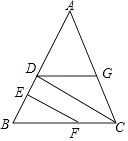
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠OAB=45°,点A的坐标是(4,0),AB= ![]() ,连结OB.
,连结OB.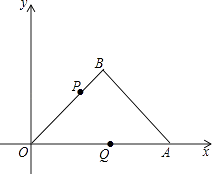
(1)直接写出点B的坐标.
(2)动点P从点O出发,沿折线O﹣B﹣A方向向终点A匀速运动,另一动点Q从点O出发,沿OA方向匀速运动,若点P的运动速度为 ![]() 个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
个单位/秒,点Q的运动速度是1个单位/秒,P、Q两点同时出发,设运动时间为t秒,请求出使△OPQ的面积等于1.5时t的值.
(3)动点P仍按(2)中的方向和速度运动,但Q点从A点向O点运动,速度为1个单位/秒,P、Q与△OAB中的任意一个顶点形成直角三角形时,求此时t(t≠0)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O在直径,AD、BC分别切⊙O于A、B两点,CD切⊙O于点E,连接OD、OC,下列结论:①∠DOC=90°,②AD+BC=CD,③S△AOD:S△BOC=AD2:AO2,④OD:OC=DE:EC,⑤OD2=DECD,正确的有( )
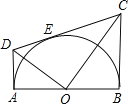
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com