
【题目】已知抛物线y=kx2+(1﹣2k)x+1﹣3k与x轴有两个不同的交点A、B.
(1)求k的取值范围;
(2)证明该抛物线一定经过非坐标轴上的一点M,并求出点M的坐标;
(3)当![]() <k≤8时,由(2)求出的点M和点A,B构成的△ABM的面积是否有最值?若有,求出该最值及相对应的k值.
<k≤8时,由(2)求出的点M和点A,B构成的△ABM的面积是否有最值?若有,求出该最值及相对应的k值.
【答案】(1)![]() 且
且![]() ;(2)见解析,M(3,4) ;(3)△ABM的面积有最大值
;(2)见解析,M(3,4) ;(3)△ABM的面积有最大值![]() ,
,![]()
【解析】
(1)根据题意得出△=(1-2k)2-4×k×(1-3k)=(1-4k)2>0,得出1-4k≠0,解不等式即可;
(2)y= k(x2-2x-3)+x+1,故只要x2-2x-3=0,那么y的值便与k无关,解得x=3或x=-1(舍去,此时y=0,在坐标轴上),故定点为(3,4);
(3)由|AB|=|xA-xB|得出|AB|=|![]() |,由已知条件得出
|,由已知条件得出![]() ,得出0<|
,得出0<|![]() |≤
|≤![]() ,因此|AB|最大时,|
,因此|AB|最大时,|![]() |=
|=![]() ,解方程即可得到结果.
,解方程即可得到结果.
解:(1)当![]() 时,函数为一次函数,不符合题意,舍去;
时,函数为一次函数,不符合题意,舍去;
当![]() 时,
时,![]() 抛物线
抛物线![]() 与
与![]() 轴相交于不同的两点
轴相交于不同的两点![]() 、
、![]() ,
,
![]() △
△![]() ,
,
![]() ,
,
![]() ,
,
∴k的取值范围为![]() 且
且![]() ;
;
(2)证明:![]() 抛物线
抛物线![]() ,
,
![]() ,
,
抛物线过定点说明在这一点![]() 与k无关,
与k无关,
显然当![]() 时,
时,![]() 与k无关,
与k无关,
解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,定点坐标为
,定点坐标为![]() ;
;
当![]() 时,
时,![]() ,定点坐标为
,定点坐标为![]() ,
,
∴M不在坐标轴上,
![]() ;
;
(3)![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 最大时,
最大时,![]() ,
,
解得:![]() ,或
,或![]() (舍去),
(舍去),
![]() 当
当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,
此时![]() 的面积最大,没有最小值,
的面积最大,没有最小值,
则面积最大为:![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】一辆货车早晨7∶00出发,从甲地驶往乙地送货.如图是货车行驶路程y(km)与行驶时间x(h)的完整的函数图像(其中点B、C、D在同一条直线上),小明研究图像得到了以下结论:
①甲乙两地之间的路程是100 km;
②前半个小时,货车的平均速度是40 km/h;
③8∶00时,货车已行驶的路程是60 km;
④最后40 km货车行驶的平均速度是100 km/h;
⑤货车到达乙地的时间是8∶24,
其中,正确的结论是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠MON=40°,OE平分∠MON,A,B,C分别是射线OM,OE,ON上的动点(A,B,C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图①,若AB∥ON,则
①∠ABO的度数是________.
②当∠BAD=∠ABD时,x=________;当∠BAD=∠BDA时,x=________.
(2)如图②,若AB⊥OM,则是否存在这样的x值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
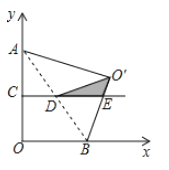
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 为
为![]() 轴正半轴上一动点,连接
轴正半轴上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得
翻折得![]() ,点
,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,点
为直角三角形时,点![]() 坐标为_______.
坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A是函数y=![]() (x>0)上一动点,连接OA,线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,将线段OA绕点A逆时针旋转90°得线段DA.
(x>0)上一动点,连接OA,线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,将线段OA绕点A逆时针旋转90°得线段DA.

(1)在图1中画出线段OB、OC,保留作图痕迹;
(2)连接AB、BC、AC,当△AOB的面积等于△BOC的面积时,求△ABC的面积;
(3)如图3,若点D的坐标为(m,n),直接写出m与n的等量关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
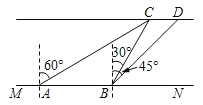
【题目】小明想要测量水面人工岛上两棵小树CD的距离,如图,已知河岸MN∥CD,小明在河岸MN上点A处测量小树C位于北偏东60°方向,然后沿河岸走了20米,到达点B处,此时测得河对岸小树C位于北偏东30°方向,小树D位于东北方向,则两棵树CD的距离为_____米.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B两小区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
(信息一)A小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
(信息二)图中,从左往右第四组的成绩如下
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
A | 75.1 | 79 | 40% | 277 | |
B | 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求A小区50名居民成绩的中位数.
(2)请估计A小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析A,B两小区居民掌握垃圾分类知识的情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,给出定义如下
+1,给出定义如下
我们称使等式a﹣b=ab+1成立的一对有理数“a,b”为共生有理数对”,记为(a,b)
(1)通过计算判断数对“﹣2,1”,“4,![]() ”是不是“共生有理数对”;
”是不是“共生有理数对”;
(2)若(6,a)是“共生有理数对”,求a的值;
(3)若(m,n)是“共生有理数对”,则“﹣n,﹣m” “共生有理数对”(填“是”或“不是”),并说明理由;
(4)若(m,n)是“共生有理数对”(其中n≠1),直接用含n的代数式表示m.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com