
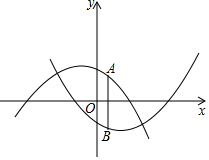
 若我们规定二次函数y1=ax2+bx+c(α≠0)的″负相关函数″为y2=-ax2+bx-c.
若我们规定二次函数y1=ax2+bx+c(α≠0)的″负相关函数″为y2=-ax2+bx-c.分析 (1)根据新定义可得;
(2)将点M(m,n)代入y1=2x2+x-3得n=2m2+m-3,即-2(-m)2+(-m)+3=-n,从而得证;
(3)设A(a,-2a2+a+3),知B(a,2a2+a-3),从而得AB的长=(-2a2+a+3)-(2a2+a-3)=-4a2+6,根据由$\left\{\begin{array}{l}{{y}_{1}=2{x}^{2}+x-3}\\{{y}_{2}=-2{x}^{2}+x+3}\end{array}\right.$得x=±$\frac{\sqrt{6}}{2}$,即可知-$\frac{\sqrt{6}}{2}$<a<$\frac{\sqrt{6}}{2}$,从而得出答案.
解答 解:(1)二次函数y1=2x2+x-3的″负相关函数″y2=-2x2+x+3;
(2)∵点M(m,n)在二次函数y1=2x2+x-3的图象上,
∴n=2m2+m-3,
∴-2(-m)2+(-m)+3=-n,
∴点M′(-m,-n)在y2=-2x2+x+3上;
(3)设A(a,-2a2+a+3),
∵线段AB平行于y轴,
∴B(a,2a2+a-3),
则AB的长=(-2a2+a+3)-(2a2+a-3)
=-4a2+6,
由$\left\{\begin{array}{l}{{y}_{1}=2{x}^{2}+x-3}\\{{y}_{2}=-2{x}^{2}+x+3}\end{array}\right.$得x=±$\frac{\sqrt{6}}{2}$,
∴-$\frac{\sqrt{6}}{2}$<a<$\frac{\sqrt{6}}{2}$,
∴当a=0时,线段AB的长度取得最大值,最大值为6.
点评 本题主要考查二次函数的性质及新定义的理解,根据新定义得出负相关函数的解析式及表示出线段AB的解析式是解题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:解答题
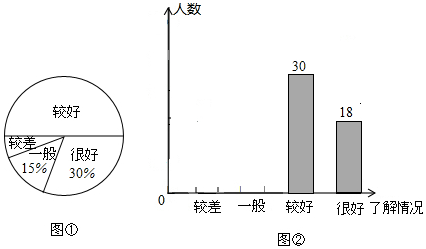
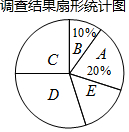 近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表
近年来,我国很多地区持续出现雾霾天气.某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表| 组别 | 观点 | 频数(人数) |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 40 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 120 |
| E | 其他 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
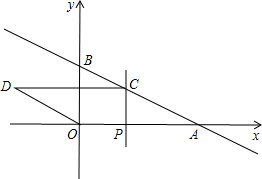 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造?OACD,设点P的横坐标为m.
如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P是x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA,AC为边构造?OACD,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
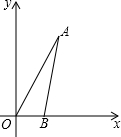 如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6. 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.
如图,在平面直角坐标系中,∠AOB=60°,点B坐标为(2,0),线段OA的长为6. 将△AOB绕点O逆时针旋转60°后,点A落在点C处,点B落在点D处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A在y轴上,坐标为(0,3),点B在x轴上.
如图,在平面直角坐标系中,点A在y轴上,坐标为(0,3),点B在x轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com