
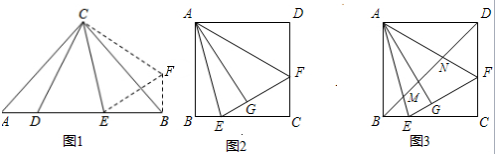
分析 探究发现:由△ECF≌△ECD(SAS),推出DE=EF,在Rt△EBF中,因为EF2=EB2+BF2,又BF=AD,EF=DE,即可推出AD2+BE2=DE2解决问题.
(1)由Rt△AEB≌Rt△AEG,推出∠EAB=∠EAG,同理可证Rt△AFD≌Rt△AFG,推出∠FAD=∠FAG,由2∠EAG+2∠FAG=90°,推出∠EAG+∠FAG=45°,推出∠EAF=45°.
(2)由探究发现得BM2+DN2=MN2,设MN=x,由BD=4,BM=1,推出DN=4-1-x=3-x,可得方程12+(3-x)2=x2,解方程即可解决问题.
解答 探究发现:解:如图1中,将△CAD绕点C逆时针旋转90°得到△CBF,连接EF.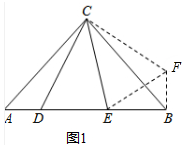
∵CA=CB,∠ACB=90°,
∴∠A=∠CBA=∠CBH=45°,
∴∠EBF=90°,
∵∠DCE=45°,
∴∠ACD+∠BCE=∠BCF+∠BCE=45°,
∴∠ECD=∠ECF,
在△ECF和△ECD中,
$\left\{\begin{array}{l}{EC=EC}\\{∠ECF=∠ECD}\\{CF=CD}\end{array}\right.$,
∴△ECF≌△ECD(SAS),
∴DE=EF,
在Rt△EBF中,∵EF2=EB2+BF2,
又∵BF=AD,EF=DE,
∴AD2+BE2=DE2,
故答案分别为△CED,SAS,AD2+BE2=DE2.
(1)解:如图2中,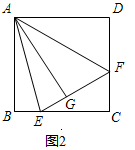
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵AG⊥EF,
∴∠AGE=∠B=90°,
在Rt△AEB和Rt△AEG中,
$\left\{\begin{array}{l}{AE=AE}\\{AB=AG}\end{array}\right.$,
∴Rt△AEB≌Rt△AEG,
∴∠EAB=∠EAG,
同理可证Rt△AFD≌Rt△AFG,
∴∠FAD=∠FAG,
∴2∠EAG+2∠FAG=90°,
∴∠EAG+∠FAG=45°,
∴∠EAF=45°.
(2)如图3中,
由(1)可知△MAN=45°,
∵AB=AD,∠BAD=90°,
由探究发现得BM2+DN2=MN2,
设MN=x,∵BD=4,BM=1,
∴DN=4-1-x=3-x,
∴12+(3-x)2=x2,
解得x=$\frac{5}{3}$,
∴MN=$\frac{5}{3}$.
点评 本题考查正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题关键是学会用旋转法添加辅助线,构造全等三角形解决问题,学会利用探究的结论解决新的问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 若我们规定二次函数y1=ax2+bx+c(α≠0)的″负相关函数″为y2=-ax2+bx-c.
若我们规定二次函数y1=ax2+bx+c(α≠0)的″负相关函数″为y2=-ax2+bx-c.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5+2b}{a}$是多项式 | B. | -7πa2的系数是-7π | ||
| C. | 4x2y2-72x3+52是5次多项式 | D. | 单项式y的系数和次数都是零 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
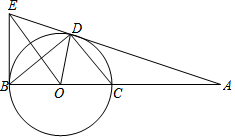 如图,BC是O的直径,A是BC延长线上一点,AE、BE分别与⊙O相切于点D、B,连接BD,CD,EO.
如图,BC是O的直径,A是BC延长线上一点,AE、BE分别与⊙O相切于点D、B,连接BD,CD,EO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 绝对值等于其本身的有理数只有0,1 | |
| B. | 相反数等于其本身的有理数只有零 | |
| C. | 倒数等于其本身的有理数只有1 | |
| D. | 最小的数是零 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com