

分析 (1)根据配方法,可得顶点坐标,根据自变量与函数值的对应关系,可得答案,根据待定系数法,可得函数解析式;
(2)根据线段垂直平分线的性质,线段的性质,可得E的坐标,根据平行于y的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PQ,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;
(3)根据勾股定理,可得关于d的方程,根据解方程,可得答案.
解答 解:(1)y=$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$=$\frac{\sqrt{3}}{3}$(x+1)2-$\frac{4\sqrt{3}}{3}$,顶点D的坐标为(-1,-$\frac{4\sqrt{3}}{3}$),
当y=0时,$\frac{\sqrt{3}}{3}$x2+$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$=0,解得x1=-3,x2=1,
∴A(-3,0),B(1,0).
当x=0时,y=-$\sqrt{3}$,
∴C(0,-$\sqrt{3}$),
∴直线AC的解析式为y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$
(2)∵△CPE得周长为BC+CE+BE,其中BC的长是固定的,
∴周长取得最小值就是BE+CE取得最小值,
∵点E是抛物线对称轴上一点,
∴BE=AE,
∴BE+CE=AE+CE,
∴BE+CE的最小值是AC,点E是AC与对称轴的交点.
∴点E为(-1,-$\frac{2\sqrt{3}}{3}$).
∵点P是抛物线上x轴下方一点,设点P为(t,$\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t-$\sqrt{3}$).且$\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t-$\sqrt{3}$<0.
过点P作QP⊥x轴交直线AC于点Q,点Q坐标为(t,-$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$).
当点p在对称轴左侧时,S△PCE=S△PCQ-S△PEQ=$\frac{1}{2}$PQ(0-t)-$\frac{1}{2}$PQ(-1-t)=$\frac{1}{2}$PQ,
当点P在对称轴的右侧时,S△PCE=S△PCQ+S△PEQ=$\frac{1}{2}$PQ(0-t)+$\frac{1}{2}$PQ[t-(-1)]=$\frac{1}{2}$PQ,
∵PQ=(-$\frac{\sqrt{3}}{3}$t-$\sqrt{3}$)-($\frac{\sqrt{3}}{3}$t2+$\frac{2\sqrt{3}}{3}$t-$\sqrt{3}$)=-$\frac{\sqrt{3}}{3}$t2-$\sqrt{3}$t,
∴S△PCE=$\frac{1}{2}$PQ=-$\frac{\sqrt{3}}{6}$t2-$\frac{\sqrt{3}}{2}$t=-$\frac{\sqrt{3}}{6}$(t+$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{8}$.
当t=-$\frac{3}{2}$时,△PEC的面积最大,最大值是$\frac{3\sqrt{3}}{8}$,此时,点P的坐标为(-$\frac{3}{2}$,-$\frac{5\sqrt{3}}{4}$);
(3)经过点P且平行于AC的直线MN的解析式为y=-$\frac{\sqrt{3}}{3}$x-$\frac{7\sqrt{3}}{4}$,
当x=0时,y=-$\frac{7\sqrt{3}}{4}$,即N(0,-$\frac{7\sqrt{3}}{4}$),当y=0时,x=-$\frac{21}{4}$,即M(-$\frac{21}{4}$,0),
设点D′的坐标为(-1,d),则MN2=(-$\frac{21}{4}$)2+(-$\frac{7\sqrt{3}}{4}$)2=$\frac{147}{4}$,MD′2=[-$\frac{21}{4}$-(-1)]2+d2=$\frac{289}{16}$+d2,ND′2=(-1)2+(-$\frac{7\sqrt{3}}{4}$-d)2=d2+$\frac{7\sqrt{3}}{2}$d+$\frac{163}{16}$.
当∠MD′N=90°时,MD′2+ND′2=MN2,即$\frac{289}{16}$+d2+d2+$\frac{7\sqrt{3}}{2}$d+$\frac{163}{16}$=$\frac{147}{4}$,
整理,得4d2+7$\sqrt{3}$d-17=0,解得d1=$\frac{-7\sqrt{3}+\sqrt{419}}{8}$,d2=$\frac{-7\sqrt{3}-\sqrt{419}}{8}$,
当∠NMD′=90°时,MD′2=ND′2+MN2,即$\frac{289}{16}$+d2=d2+$\frac{7\sqrt{3}}{2}$d+$\frac{163}{16}$+$\frac{147}{4}$,
化简,得$\frac{7\sqrt{3}}{2}$d=-$\frac{231}{8}$,解得d=-$\frac{11\sqrt{3}}{4}$,
当∠NMD′-90°时,ND′2=MD′2+MN2,即d2+$\frac{7\sqrt{3}}{2}$d+$\frac{163}{16}$=$\frac{289}{16}$+d2+$\frac{147}{4}$,
化简,得$\frac{7\sqrt{3}}{2}$d=$\frac{357}{8}$,解得d=$\frac{17\sqrt{3}}{4}$,
∴存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,D′点的坐标为(-1,$\frac{-7\sqrt{3}+\sqrt{419}}{8}$)(-1,$\frac{-7\sqrt{3}-\sqrt{419}}{8}$),(-1,$\frac{-11\sqrt{3}}{4}$)(-1$\frac{17\sqrt{3}}{4}$).
点评 本题考查了二次函数综合题,解(1)的关键是配方法得出顶点坐标,又利用了待定系数法求函数解析式;解(2)的关键利用线段垂直平分线的性质,线段的性质得出E的坐标,又利用了平行于y的直线上两点间的距离是较大的纵坐标减较小的纵坐标得出PQ的长;解(3)的关键是利用勾股定理得出关于d的方程,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:解答题
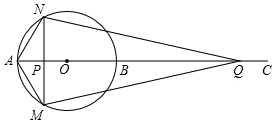 如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.
如图,AB为⊙O的直径,点C为AB延长线上一点,动点P从点A出发沿AC方向以1cm/s的速度运动,同时动点Q从点C出发以相同的速度沿CA方向运动,当两点相遇时停止运动,过点P作AB的垂线,分别交⊙O于点M和点N,已知⊙O的半径为$\frac{3}{2}$cm,AC=8cm,设运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
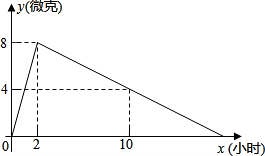 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10-3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
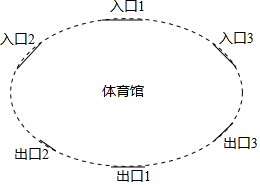 某体育馆有3个入口和3个出口,其示意图如下,参观者可从任意一个入口进入,参观结束后从任意一个出口离开
某体育馆有3个入口和3个出口,其示意图如下,参观者可从任意一个入口进入,参观结束后从任意一个出口离开查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 折纸三等分角 三等分角问题(trisection of an angle)是二千四百年前,古希腊人提出的几何三大作图问题之一(三等分任意角、化圆为方、倍立方),即用圆规与直尺(没有刻度,只能做直线的尺子)把一任意角三等分,这问题曾吸引着许多人去研究,但无一成功.1837年法国数学家凡齐尔(1814~1848)运用代数方法证明了,仅用尺规不可鞥呢三等分角. 如果作图工具没有限制,将条件放宽,将任意角三等分是可以解决的.下面介绍一种折纸三等分任意锐角的方法: (1)在正方形纸片上折出任意∠SBC,将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,得到图(1); (2)翻折左下角使点B与EF上的点T重合,点M与SB上的点P重合,点E对折后的对应点记为Q,折痕为记为GH,得到图(2); (3)折出射线BQ,BT,得到图(3),则射线BQ,BT就是∠SBC的三等分线.  下面是证明BQ,BT是∠SBC三等分线的部分过程: 证明:过T作TK⊥BC,垂足为K,则四边形EBKT为矩形 根据折叠,得EB=QT,∠EBT=∠QTB,BT=TB ∴△EBT≌△QTB, ∴∠BQT=∠TEB=90°, ∴BQ⊥PT … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com