
【题目】如图,已知直线AB的函数解析式为y=2x+10,与y轴交于点A,与x轴交于点B.

(1)求A,B两点的坐标;
(2)若点P(a,b)为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,问:
①若△PBO的面积为S,求S关于a的函数解析式;
②是否存在点P,使EF的值最小?若存在,求出EF的最小值;若不存在,请说明理由.
【答案】(1)A(0,10),B(-5,0);(2)①S=5a+25(-5≤a≤0);②存在点P使得EF的值最小,最小值为2![]() .
.
【解析】(1)由直线AB解析式,令x=0与y=0分别求出y与x的值,即可确定出A与B的坐标;
(2)①把P坐标代入直线AB解析式,得到a与b的关系式,三角形POB面积等于OB为底边,P的纵坐标为高,表示出S与a的解析式即可;
②存在,理由为:利用三个角为直角的四边形为矩形,得到四边形PFOE为矩形,利用矩形的对角线相等得到EF=PO,由O为定点,P为动点,得到OP垂直于AB时,OP取得最小值,利用面积法求出OP的长,即为EF的最小值.
(1)对于直线AB的解析式y=2x+10,
令x=0,得到y=10,
令y=0,得到x=-5,
则A(0,10),B(-5,0);
(2)连接OP,如图,

①∵P(a,b)在线段AB上,∴b=2a+10,
由0≤2a+10≤10,得到-5≤a≤0,
由(1)得OB=5,
∴![]() =
=![]() OB·(2a+10),
OB·(2a+10),
则S=![]() (2a+10)=5a+25(-5≤a≤0);
(2a+10)=5a+25(-5≤a≤0);
②存在,理由:
∵∠PFO=∠FOE=∠OEP=90°,
∴四边形PFOE为矩形,∴EF=PO,
∵O为定点,P在线段AB上运动,
∴当OP⊥AB时,OP取得最小值,
∵![]() AB·OP=
AB·OP=![]() OB·OA,
OB·OA,
即![]() ×5
×5![]() ·OP=
·OP=![]() ×5×10,解得OP=2
×5×10,解得OP=2![]() ,
,
∴EF=OP=2![]() ,
,
综上,存在点P使得EF的值最小,最小值为2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】周末,小明,小红等同学随父母一同去某景点旅游,在购买门票时,小明和小红有图1所示的对话,根据图2的门票票价和图1所示的对话内容完成下列问题.
(1)他们一共去了几个成人几个学生?
(2)请你帮他们算一算,用哪种方式买票更省钱,省多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
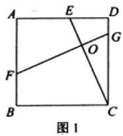
【题目】如图1,在正方形ABCD中,点E为AD上一点,FG⊥CE分别交AB、CD于F、G,垂足为O.
(1)求证:CE=FG;
(2)如图2,连接OB,若AD=3DE,∠OBC=2∠DCE。
求![]() 的值;
的值;
若AD=3,则OE的长为_________(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.
(1)求该抛物线的函数解析式;
(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.
①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH的面积;
②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店第一次用400元购进胶皮笔记本若干个,第二次又用400元购进该种型号的笔记本,但这次每个的进价是第一次进价的1.25倍,购进数量比第一次少了20个.
(1)求第一次每个笔记本的进价是多少?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后后获利不低于460元,问每个笔记本至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.
因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果.
解:1+2+3+…+100=(1+100)+(2+99)+(3+98)+…+(50+51)=![]() =5050.
=5050.
(1)补全例题![]() 解题过程;
解题过程;
(2)计算a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为⊙O的直径,A为圆上一点,点F为 ![]() 的中点,延长AB、AC,与过F点的切线交于D、E两点.
的中点,延长AB、AC,与过F点的切线交于D、E两点. 
(1)求证:BC∥DE;
(2)若BC:DF=4:3,求tan∠ABC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com