
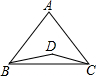
 如图,已知AB=AC,BD=CD,∠BDC=150°,∠ABD=40°,求∠BAC的度数.
如图,已知AB=AC,BD=CD,∠BDC=150°,∠ABD=40°,求∠BAC的度数. 科目:初中数学 来源: 题型:解答题
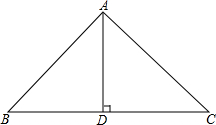 若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.
若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形过该顶点的生成三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
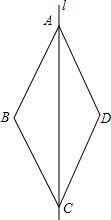 如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.
如图,直线l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AD=DC.其中正确的结论是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
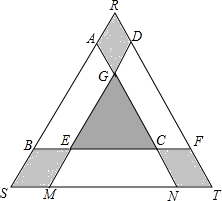 某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.
某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com