
【题目】如图,E,F是平行四边形ABCD的对角线AC上的点,CE=AF.请你猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证明: 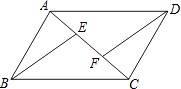
【答案】BE∥DF,BE=DF|连接BD,交AC于点O,连接DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO,
又∵AF=CE,
∴AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
∴BE∥DF,BE=DF
【解析】答:猜想:BE∥DF,BE=DF.证明:证法一:如图1,
∵四边形ABCD是平行四边形.
∴BC=AD,∠1=∠2,
∵在△BCE和△DAF中,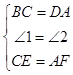 ,
,
∴△BCE≌△DAF(SAS),
∴BE=DF,∠3=∠4,
∴BE∥DF.
证法二:如图2,
连接BD,交AC于点O,连接DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO,
又∵AF=CE,
∴AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
∴BE∥DF,BE=DF.
故答案为:BE∥DF,BE=DF;
连接BD,交AC于点O,连接DE,BF.
∵四边形ABCD是平行四边形,
∴BO=OD,AO=CO,
又∵AF=CE,
∴AE=CF,
∴EO=FO,
∴四边形BEDF是平行四边形,
∴BE∥DF,BE=DF.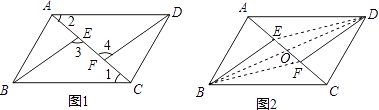
首先连接BD,交AC于点O,连接DE,BF.由四边形ABCD是平行四边形,可得BO=OD,AO=CO,又由CE=AF,可得OE=OF,即可证得四边形BEDF是平行四边形,则可得BE∥DF,BE=DF


科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论: ①AM=CN;
②∠AME=∠BNE;
③BN﹣AM=2;
④S△EMN= ![]() .
.
上述结论中正确的个数是( )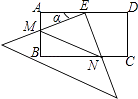
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( ) 
A.abc<0
B.2a+b<0
C.a﹣b+c<0
D.4ac﹣b2<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形一定是平行四边形
B.对角线相等的四边形一定是矩形
C.两条对角线互相垂直的四边形一定是菱形
D.两条对角线相等且互相垂直平分的四边形一定是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF= ![]() ,BD=4,则菱形ABCD的周长为( )
,BD=4,则菱形ABCD的周长为( ) 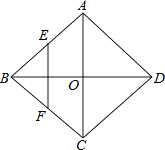
A.4
B.4 ![]()
C.4 ![]()
D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE= ![]() BC,求证:四边形ABFC为矩形;
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,直接写出当△ABC再满足时,四边形ABFC为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.
(1)求圆的半径及圆心P的坐标;
(2)M为劣弧 ![]() 的中点,求证:AM是∠OAB的平分线;
的中点,求证:AM是∠OAB的平分线;
(3)连接BM并延长交y轴于点N,求N,M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com