
【题目】如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE= ![]() BC,求证:四边形ABFC为矩形;
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,直接写出当△ABC再满足时,四边形ABFC为正方形.
【答案】
(1)
证明:∵四边形ABCD为平行四边形,
∴AB∥DC,
∴∠ABE=∠ECF,
又∵E为BC的中点,
∴BE=CE,
在△ABE和△FCE中,
∵ 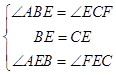 ,
,
∴△ABE≌△FCE(ASA)
(2)
证明:∵△ABE≌△FCE,
∴BE=EC,AE=EF,
∴四边形ABFC为平行四边形,
又∵AE= ![]() BC,
BC,
∴AF=BC,
∴四边形ABFC为矩形
(3)AB=AC
【解析】证明: (3)当△ABC为等腰三角形时,即AB=AC时,四边形ABFC为正方形;
理由如下:
∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵四边形ABFC为平行四边形,
∴四边形ABFC是菱形,
又∵四边形ABFC是矩形,
∴四边形ABFC为正方形.
所以答案是:AB=AC.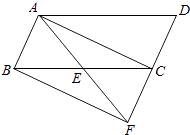
【考点精析】解答此题的关键在于理解全等三角形的性质的相关知识,掌握全等三角形的对应边相等; 全等三角形的对应角相等.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.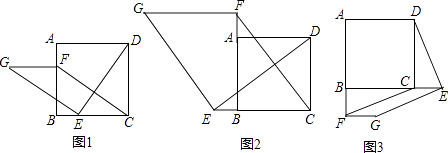
(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD各边中点,得到四边形A1B1C1D1 , 再顺次连接四边形A1B1C1D1各边中点,得到四边形A2B2C2D2 , …,如此进行下去,得到四边形AnBnCnDn . 下列结论正确的有( )
①四边形A2B2C2D2是矩形;
②四边形A4B4C4D4是菱形;
③四边形A5B5C5D5的周长是 ![]() ,
,
④四边形AnBnCnDn的面积是 ![]() .
.
A.①②③
B.②③④
C.①②
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△ACD,点O、B对应点分别是C、D. 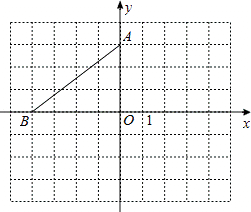
(1)若点B的坐标是(﹣4,0),请在图中画出△ACD,并写出点C、D的坐标;
(2)当点D落在第一象限时,试写出一个符合条件的点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代《易经》一书中记载,远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )
A.84
B.336
C.510
D.1326
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() .
.
(1)若该反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,求k的值;
(2)如图,反比例函数y= ![]() (1≤x≤4)的图象记为曲线C1 , 将C1向左平移2个单位长度,得曲线C2 , 请在图中画出C2 , 并直接写出C1平移至C2处所扫过的面积.
(1≤x≤4)的图象记为曲线C1 , 将C1向左平移2个单位长度,得曲线C2 , 请在图中画出C2 , 并直接写出C1平移至C2处所扫过的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com