
【题目】平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△ACD,点O、B对应点分别是C、D. 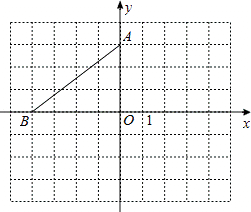
(1)若点B的坐标是(﹣4,0),请在图中画出△ACD,并写出点C、D的坐标;
(2)当点D落在第一象限时,试写出一个符合条件的点B的坐标.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+ ![]() )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.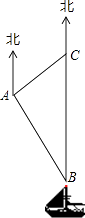
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于O点,E,F分别是AB,BC边上的中点,连接EF.若EF= ![]() ,BD=4,则菱形ABCD的周长为( )
,BD=4,则菱形ABCD的周长为( ) 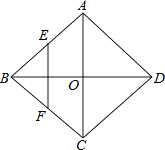
A.4
B.4 ![]()
C.4 ![]()
D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE= ![]() BC,求证:四边形ABFC为矩形;
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,直接写出当△ABC再满足时,四边形ABFC为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+m﹣4经过点A(5,﹣5),若抛物线顶点为P.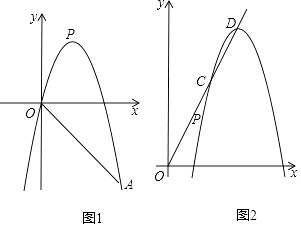
(1)求点P的坐标;
(2)在直线OA上方的抛物线上任取一点M,连接MO、MA,求△MOA的面积取得最大时的点M坐标;
(3)如图1,将原抛物线沿射线OP方向进行平移得到新的抛物线,新抛物线与射线OP交于C、D两点.试问线段CD的长度是否为定值,若是请求出这个定值;若不是请说明理由.(提示:若点C(x1 , y1),D(x2 , y2),则CD的长度d= ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某商店购买商品A、B共两次,这两次购买商品A、B的数量和费用如表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购物 | 4 | 3 | 93 |
第二次购物 | 6 | 6 | 162 |
若小丽需要购买3个商品A和2个商品B,则她要花费( )
A.64元
B.65元
C.66元
D.67元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com