
����Ŀ����ͼ���ı���ABCD�У�AC=a��BD=b����AC��BD��˳�������ı���ABCD�����е㣬�õ��ı���A1B1C1D1 �� ��˳�������ı���A1B1C1D1�����е㣬�õ��ı���A2B2C2D2 �� ������˽�����ȥ���õ��ı���AnBnCnDn �� ���н�����ȷ���У� ��
���ı���A2B2C2D2�Ǿ��Σ�
���ı���A4B4C4D4�����Σ�
���ı���A5B5C5D5���ܳ��� ![]() ��
��
���ı���AnBnCnDn������� ![]() ��
��
A.�٢ڢ�
B.�ڢۢ�
C.�٢�
D.�ڢ�
���𰸡�B
���������⣺������A1C1 �� B1D1 �� �����ı���ABCD�У�˳�������ı���ABCD �����е㣬�õ��ı���A1B1C1D1 ��
��A1D1��BD��B1C1��BD��C1D1��AC��A1B1��AC��
��A1D1��B1C1 �� A1B1��C1D1 ��
���ı���A1B1C1D1��ƽ���ı��Σ�
��AC�ABD�����ı���A1B1C1D1�Ǿ��Σ�
��B1D1=A1C1�����ε������Խ�����ȣ���
��A2D2=C2D2=C2B2=B2A2����λ�߶�������
���ı���A2B2C2D2�����Σ�
�ʱ�ѡ������ɢ�֪���ı���A2B2C2D2�����Σ�
�������λ�߶���֪���ı���A4B4C4D4�����Σ�
�ʱ�ѡ����ȷ���۸�����λ�ߵ�������֪��A5B5= ![]() A3B3=
A3B3= ![]() A1B1=
A1B1= ![]() AC��B5C5=
AC��B5C5= ![]() B3C3=
B3C3= ![]() B1C1=
B1C1= ![]() BD��
BD��
���ı���A5B5C5D5���ܳ���2�� ![]() ��a+b��=
��a+b��= ![]() ��
��
�ʱ�ѡ����ȷ���ܡ��ı���ABCD�У�AC=a��BD=b����AC�ABD��
��S�ı���ABCD=ab��2��
�������ε���λ�ߵ����ʿ�����֪��ÿ�õ�һ���ı��Σ����������Ϊԭ����һ�룬
�ı���AnBnCnDn������� ![]() ��
��
�ʱ�ѡ����ȷ��
�����������ڢۢ���ȷ��
��ѡ��B��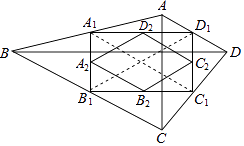



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA=3��OC=2����F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y= ![]() ��ͼ����BC�߽��ڵ�E��
��ͼ����BC�߽��ڵ�E�� 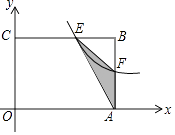
��1����FΪAB���е�ʱ����ú����Ľ���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ���װ�к졢�ơ���������ɫ����100�������dz���ɫ�ⶼ��ͬ�����л���ĸ����ǰ��������2����5������֪�Ӵ�������һ������ĸ����� ![]() ��
��
��1������к���ĸ�����
��2����Ӵ�������һ�����ǰ���ĸ��ʣ�
��3��ȡ��5������5���������ʣ�����������һ�����Ǻ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.һ��Ա���ȣ���һ��Ա�ƽ�е��ı���һ����ƽ���ı���
B.�Խ�����ȵ��ı���һ���Ǿ���
C.�����Խ����ഹֱ���ı���һ��������
D.�����Խ�������һ��ഹֱƽ�ֵ��ı���һ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ABC�У���O��AC���ϵ�һ�����㣬����O��ֱ��MNƽ����BC����MN��BCA��ƽ�����ڵ�E������BCA�����ƽ�����ڵ�F�� 
��1����˵����EO=FO��
��2������O�˶����δ�ʱ���ı���AECF�Ǿ��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��ƽ���ı���ABCD��BC�ߵ��е㣬����AE���ӳ�AE��DC���ӳ����ڵ�F��
��1����֤����ABE�ա�FCE��
��2������AC��BF����AE= ![]() BC����֤���ı���ABFCΪ���Σ�
BC����֤���ı���ABFCΪ���Σ�
��3���ڣ�2�������£�ֱ��д������ABC������ʱ���ı���ABFCΪ�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ش���������⣺
�ⷽ�̣�x2��|x|��2=0��
�⣺��x��0ʱ��ԭ���̻�Ϊx2��x��2=0�����x1=2��x2=��1���������⣬��ȥ����
��x��0ʱ��ԭ���̻�Ϊx2+x��2=0�����x1=��2��x2=1���������⣬��ȥ����
��ԭ���̵ĸ���x1=2��x2=��2��
���������ⷽ��x2+|x��4|��8=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���OΪ����ԭ�㣬��B������Ϊ��4��3������A��C���������ϣ���P��BC���ϣ�ֱ��l1��y=2x+3��ֱ��l2��y=2x��3��
��1���ֱ���ֱ��l1��x�ᣬֱ��l2��AB�Ľ������ꣻ
��2����֪��M�ڵ�һ���ޣ�����ֱ��l2�ϵĵ㣬����APM�ǵ���ֱ�������Σ����M�����ꣻ
��3�����ǰ�ֱ��l1��ֱ��l2�ϵĵ�����ɵ�ͼ��Ϊͼ��F����֪����ANPQ�Ķ���N��ͼ��F�ϣ�Q������ƽ���ڵĵ㣬��N��ĺ�����Ϊx����ֱ��д��x��ȡֵ��Χ������˵�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�EΪ��CD��һ�㣬����ADE��AE�۵�����AD��E����AD����CE���ڵ�F������B=52�㣬��DAE=20�㣬���FED��Ĵ�СΪ �� 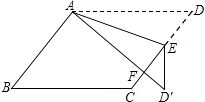
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com