
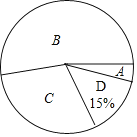
����Ŀ����ͼ1������BPCƽ���ߵķ����ӳ���PA����Ҫ�ֱ��ԡ�APB����APC����BPCΪ�ڽ���������Σ��ұ߳���Ϊ1�����������������������䲻ͬ���ƺ��Ϊһ��ͼ�������磬���ԡ�BPCΪ�ڽǣ�������һ���߳�Ϊ1�������Σ���ʱ��BPC=90������![]() =45��360�����������Ǻͣ���
=45��360�����������Ǻͣ���![]() ��������ǡ�ÿ����������߳���Ϊ1�����˱��Σ���仨�ƺ�õ�һ������Ҫ���ͼ������ͼ2��ʾ��
��������ǡ�ÿ����������߳���Ϊ1�����˱��Σ���仨�ƺ�õ�һ������Ҫ���ͼ������ͼ2��ʾ��

ͼ2�е�ͼ���������ܳ���_____��
�����з���Ҫ���ͼ����ѡһ���������ܳ����Ķ�Ϊ��꣬������������ܳ���_____��
���𰸡� 14 21
������������ͼ2����Χ����ӿɵ�ͼ���������ܳ������BPC=2x���ȱ�ʾ�м�������εı��������Ϊ180�㩁2x��������ǺͿɵñ���=![]() ��ͬ���ɵ�����������ε����Ϊx���ɵñ���Ϊ
��ͬ���ɵ�����������ε����Ϊx���ɵñ���Ϊ![]() ���������ܳ��ɵý��ۣ�
���������ܳ��ɵý��ۣ�
ͼ2�е�ͼ���������ܳ��ǣ�8��2+2+8��2=14��
���BPC=2x��
���ԡ�BPCΪ�ڽǵ�������εı���Ϊ��![]() ��
��
�ԡ�APBΪ�ڽǵ�������εı���Ϊ��![]() ��
��
��ͼ���������ܳ���=![]() ��2+
��2+![]() ��2+
��2+![]() ��2=
��2=![]() +
+![]() ��6��
��6��
���������֪��2x��ֵֻ��Ϊ60�㣬90�㣬120�㣬144�㣬
��xԽСʱ���ܳ�Խ��
�൱x=30ʱ���ܳ����ʱͼ����Ϊ��꣬
��������������ܳ���=![]() ��6=21��
��6=21��
�ʴ�Ϊ��14��21��


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��
��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��

A.�ڡ�A����B���ڽ�ƽ���ߵĽ��㴦
B.��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
C.��AC��BC���߸��ߵĽ��㴦
D.��AC��BC�������ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н���չ�����߽��й���ѧʷ��Ϊ�����֪ʶ�������������ѧУ�Ա�У100���μ�ѡ������ͬѧ�ijɼ���A��B��C��D�ĸ��ȼ�����ͳ�ƣ����Ƴ����²�������ͳ�Ʊ�������ͳ��ͼ��
�ɼ��ȼ� | Ƶ���������� | Ƶ�� |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
�ϼ� | 100 | 1 |
��1����m=�� ����n=�� ����
��2��������ͳ��ͼ�У�����C�ȼ�������Ӧ�ĽǵĶ�����
��3���ɼ��ȼ�ΪA��4��ͬѧ����1��������3��Ů�����ִ��������ѡ2��ͬѧ����ѧУ�μ�ȫ�б�����������״ͼ�������б������ǡ��ѡ����1��1Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
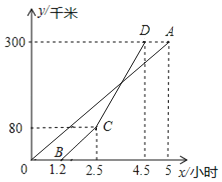
����Ŀ���ס����������300ǧ�ף�һ��������һ���γ��ֱ�Ӽؿ����ҵ�![]() �γ���ƽ���ٶȴ��ڻ�����ƽ���ٶ�
�γ���ƽ���ٶȴ��ڻ�����ƽ���ٶ�![]() ����ͼ���߶�OA������BCD�ֱ��ʾ������صľ���
����ͼ���߶�OA������BCD�ֱ��ʾ������صľ���![]() ��λ��ǧ��
��λ��ǧ��![]() ��ʱ��
��ʱ��![]() ��λ��Сʱ
��λ��Сʱ![]() ֮��ĺ�����ϵ��
֮��ĺ�����ϵ��
![]() �߶�OA������BCD�У�______��ʾ������صľ���y��ʱ��x֮��ĺ�����ϵ��
�߶�OA������BCD�У�______��ʾ������صľ���y��ʱ��x֮��ĺ�����ϵ��
![]() ���߶�CD�ĺ�����ϵʽ��
���߶�CD�ĺ�����ϵʽ��
![]() ���������ʱ������������
���������ʱ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У�����A+��B����C������A����B����C��1��5��6������A��90�㩁��B������A����B��![]() ��C�У���ȷ����ABC��ֱ�������ε������У�������
��C�У���ȷ����ABC��ֱ�������ε������У�������
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ŀ������![]() ������ϵ����
������ϵ����![]() ��ӡˢ�������
��ӡˢ�������
��1��������![]() ���³�3�����㻯��3x2+6x+8���C��6x+5x2+2����
���³�3�����㻯��3x2+6x+8���C��6x+5x2+2����
��2��������˵������´��ˣ��ҿ���������𰸵Ľ���dz�������ͨ������˵��ԭ������![]() ���Ǽ���
���Ǽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Գdz���һ��̨ʽ���Ժ�Һ����ʾ��������ÿ̨����2000Ԫ��Һ����ʾ��ÿ������400Ԫ.�����ڼ俪չ���������ͻ��ṩ�����Żݷ�����
�����٣���һ̨������һ��Һ����ʾ����
�����ڣ����Ժ�Һ����ʾ���������۵�![]() ����.
����.
��ѧУҪ�����������豸�����õ��Գǹ������30̨��Һ����ʾ��![]() ����
����![]() ����
����
��1����ѧУ�ֱ𰴷����ٻ��ڹ����踶�����Ԫ�����ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
��2����![]() ��ͨ������˵����ʱѧУ�����ַ��������Ϊ���㣿
��ͨ������˵����ʱѧУ�����ַ��������Ϊ���㣿
��3����![]() ʱ������ΪѧУ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ���.
ʱ������ΪѧУ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı����У���OΪ�Խ���BD���е㣬DE��BF�ֱ�ƽ�֡�ADC�͡�ABC.
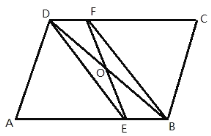
(1)��֤��EF��BD����ƽ�֣�
(2)����A=60��AE=2EB��AD=4�����ı���DEBF���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У���A=��C=90����

��1����ͼ1����BEƽ�֡�ABC��DFƽ�֡�ADC���ڲ��ǣ���д��BE��DF��λ�ù�ϵ����֤����
��2����ͼ2����BF��DE�ֱ�ƽ�֡�ABC����ADC���ڲ��ǣ��ж�DE��BFλ�ù�ϵ��֤����
��3����ͼ3����BE��DE�ֱ����ȷ֡�ABC����ADC���ڲ��ǣ�����CBE=![]() ��CBM����CDE=
��CBM����CDE=![]() ��CDN�������E= ��
��CDN�������E= ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com