
【题目】某电脑城出售一种台式电脑和液晶显示器,电脑每台定价2000元,液晶显示器每个定价400元.国庆期间开展促销活动,向客户提供两种优惠方案:
方案①:买一台电脑送一个液晶显示器;
方案②:电脑和液晶显示器都按定价的![]() 付款.
付款.
现学校要更新微机教室设备,到该电脑城购买电脑30台,液晶显示器![]() 个(
个(![]() ),
),
(1)若学校分别按方案①或方案②购买,各需付款多少元?(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,通过计算说明此时学校按哪种方案购买较为合算?
,通过计算说明此时学校按哪种方案购买较为合算?
(3)当![]() 时,你能为学校想出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能为学校想出一种更为省钱的购买方案吗?试写出你的购买方法.
【答案】(1)学校按方案①购买需付款(400x+48000)元,按方案②购买需付款(360x+54000)元;(2)当x=40时,学校按方案①购买较为合算;(3)先按方案①购买30台电脑,再按方案②购买剩余的10个液晶显示器.
【解析】
(1)根据向客户提供两种优惠方案列出代数式即可;
(2)将x=40代入求得的代数式中即可得到费用,然后比较即可得到选择哪种方案更合算;
(3)根据题意可以得到先按方案①购买30台电脑送30个液晶显示器,再按方案②购买10个液晶显示器更合算.
(1)解:按方案①购买所需费用为2000×30+400(x-30)=400x+48000
按方案②购买所需费用为90%(2000×30+400x)=360x+54000
答:学校按方案①购买需付款(400x+48000)元,按方案②购买需付款(360x+54000)元.
(2)解:当x=40时,
方案①应付费用为400×40+48000=64000元
方案②应付费用为360×40+54000=68400元
因为64000<68400
所以当x=40时,学校按方案①购买较为合算.
(3)解:能为学校想出一种更为省钱的购买方案.
先按方案①购买30台电脑,需要费用2000×30=60000元,
同时获赠30个液晶显示器.
再按方案②购买剩余的10个液晶显示器,需要费用0.9×400×10=3600元
此时共需60000+3600=63600元,费用更省.
答:先按方案①购买30台电脑,同时获赠30个液晶显示器. 再按方案②购买剩余的10个液晶显示器,费用更省.


科目:初中数学 来源: 题型:
【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt![]() ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt![]() ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
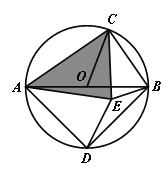
求证:![]() ACE是奇异三角形;
ACE是奇异三角形;
当![]() ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.
(1)若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)超市和姥爷家相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而![]() =45是360°(多边形外角和)的
=45是360°(多边形外角和)的![]() ,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.

图2中的图案外轮廓周长是_____;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)解方程:|3x-2|-4=0.
(2)解关于x的方程:|x-2|=b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形一边长为12cm,那么它的两条对角线的长度可以是( )
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
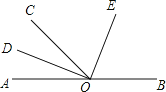
(1)请你数一数,图中有多少小于平角的角?
(2)求∠BOD的度数;
(3)试判断∠BOE和∠COE有怎样的数量关系,说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com