
����Ŀ���Ķ�������龳�Ի���Ȼ��������

��1���������������������Ķ��壬�����ж�С����������⣺���ȱ�������һ������������������������Ǽ����⣿
��2����Rt![]() ABC �� ��ACB��90����AB��c��AC��b��BC��a����b��a����Rt
ABC �У� ��ACB��90����AB��c��AC��b��BC��a����b��a����Rt![]() ABC�����������Σ���a��b��c��
ABC��������������a��b��c��
��3����ͼ��AB����O��ֱ����C����һ�㣨�����A��B�غϣ���D�ǰ�Բ���е㣬CD��ֱ��AB�����࣬������O�ڴ��ڵ�Eʹ��AE��AD��CB��CE��
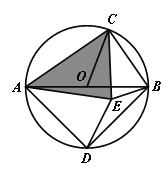
��֤��![]() ACE�����������Σ�
ACE������������
��![]() ACE��ֱ��������ʱ������AOC�Ķ�����
ACE��ֱ��������ʱ������AOC�Ķ�����
���𰸡��⣺��1��������
��2����Rt![]() ABC ��a2��b2�� c2��
ABC ��a2��b2�� c2��
��c��b��a��0
��2c2��a2��b2��2a2��c2��b2
����Rt![]() ABC�����������Σ�һ����2b2��c2�� a2
ABC�����������Σ�һ����2b2��c2�� a2
��2b2��a2����a2��b2��
��b2��2a2���ã�b��![]() a
a
��c2��b2�� a2��3a2
��c��![]()
��a��b�� c��![]()
(3)��AB����O��ֱ��ACBADB��90��
��Rt![]() ABC ��AC2��BC2��AB2
ABC ��AC2��BC2��AB2
��Rt![]() ADB ��AD2��BD2��AB2
ADB ��AD2��BD2��AB2
����D�ǰ�Բ���е�
����
��AD��BD
��AB2��AD2��BD2��2AD2
��AC2��CB2��2AD2
����CB��CE��AE��AD
��AC2��CE2��2AE2
��![]() ACE������������
ACE������������
���ɵ�![]() ACE������������
ACE������������
��AC2��CE2��2AE2
��![]() ACE��ֱ��������ʱ
ACE��ֱ��������ʱ

����������1���������������������Ķ�����ȱ������ε����ʣ���֤���ɣ�
��2�����ݹ��ɶ��������������ε����ʣ��ɵ�a2+b2=c2��a2+c2=2b2����a��ʾ��b��c��������ô𰸣�
��3����AB����O��ֱ�������������ACB=��ADB=90����Ȼ�����ù��ɶ�����Բ�����ʼ���֤�ã�
�����ã�2���еĽ��ۣ��ֱ��AC��AE��CE��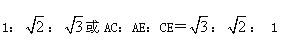 ȥ������������ý����
ȥ������������ý����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ծ���ABCD�ı�CDΪֱ������O�������εĶԽ���BD�ڵ�E����F��BC���е㣬����EF��
��1�����ж�EF���O��λ�ù�ϵ����˵�����ɣ�
��2����DC=2��EF=![]() ����P�ǡ�O�ϲ���E��C�غϵ�����һ�㣬���EPC�Ķ���Ϊ ��ֱ��д���𰸣�
����P�ǡ�O�ϲ���E��C�غϵ�����һ�㣬���EPC�Ķ���Ϊ ��ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ�����
+6����8����0.4��0��230%�� ![]() ����1
����1 ![]() ��������5������|��2|����
��������5������|��2|���� ![]() ��0.010010001������2.33��
��0.010010001������2.33��
��1���������ϣ�{}��
��2���������ϣ�{ }��
��3���������ϣ�{}��
��4�����������ϣ�{}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����
A. ÿ���ڽǶ���120���������һ�����������Σ�
B. ��n���εĶԳ��һ����n����
C. ��n���ε�ÿһ����Ƕ��������������ĽǶ�����
D. �������һ��������Գ�ͼ�Σ��������ĶԳ�ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�����ֽ���ϻ�һ�����ᣮ 
��1�����۵�ֽ���������ϱ�ʾ��3�ĵ����ʾ1�ĵ��غϣ����ۺ�������Ľ����ʾ����Ϊ��
��2��������ij���۵��������ϵ�������a��b��ʾ�ĵ�ǡ���غϣ����ۺ�������Ľ����ʾ����Ϊ���ú�a��b�Ĵ���ʽ��ʾ����
��3��������ֽ�������ߴ����������м��һ��ֽ�����ۣ�ʹ�����������غϣ�������������n�κ��ٽ���չ������ֱ��������˵��ۺۺ����Ҷ˵��ۺ�������Ľ����ʾ���������ú�n�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������7������ͼ����֪���κ���![]() ��ͼ����x�Ḻ���ύ����A��-1��0������y�������ύ���B������ΪP����OB=3OA��һ�κ���y=kx+b��ͼ��A��B��
��ͼ����x�Ḻ���ύ����A��-1��0������y�������ύ���B������ΪP����OB=3OA��һ�κ���y=kx+b��ͼ��A��B��
��1����һ�κ�������ʽ��
��2����P��������
��3��ƽ��ֱ��ABʹ�����P����������ƽ�ƺ��ֱ���ϣ���![]() �����M������
�����M������
�������������ߵĶԳ��ύx�����E������AP��y�����D������Q��N�ֱ�Ϊ���߶�PE��PD�ϵĶ��㣬����QD��QN����ֱ��д��QD+QN����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
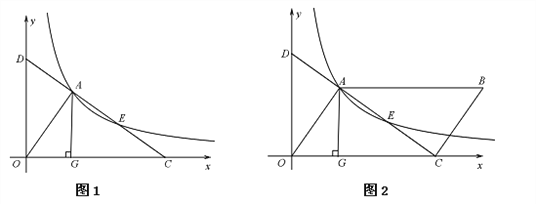
����Ŀ����ͼ1��ֱ��![]() ��x���ڵ�C����y���ڵ�D���뷴��������
��x���ڵ�C����y���ڵ�D���뷴��������![]() ��ͼ��������A��E��AG��x�ᣬ����Ϊ��G��S��AOG��3��
��ͼ��������A��E��AG��x�ᣬ����Ϊ��G��S��AOG��3��
��1��k �� ��
��2����֤��AD ��CE��
��3����ͼ2������EΪƽ���ı���OABC�ĶԽ���AC���е㣬��ƽ���ı���OABC�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����10��10�����������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ���B��C����ֱ�Ϊ����4��2��������1��2����
��1����ͼ�н���ƽ��ֱ������ϵ��д����A�����ꣻ
��2������ABC������ƽ��4����λ��������ƽ��5����λ�õ���A1B1C1 �� ������A1B1C1 �� ��д����C1�����ꣻ
��3��M��a��b���ǡ�ABC�ڵ�һ�㣬��ABC����ij�ֱ任���M�Ķ�Ӧ��ΪM2��a+1��b��7����������A2B2C2 �� �������A2B2C2�������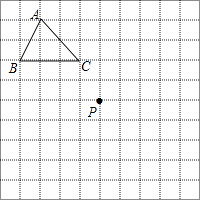
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com