
【题目】如图,以矩形ABCD的边CD为直径作⊙O,交矩形的对角线BD于点E,点F是BC的中点,连接EF.
(1)试判断EF与⊙O的位置关系,并说明理由.
(2)若DC=2,EF=![]() ,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
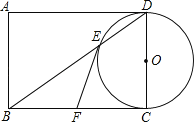
【答案】(1)EF与⊙O相切,证明见解析;(2)600或1200
【解析】(1)直线EF与⊙O相切.理由如下:如图,连接OE、OF.通过△EFO≌△CFO(SAS),证得∠FEO=∠FCO=90°,则直线EF与⊙O相切.
(2)根据圆内接四边形的性质得到∠EPC+∠D=180°,利用(1)中的全等三角形的对应边相等求得FC=EF=![]() ,所以通过解直角△BCD来求∠D的度数即可.
,所以通过解直角△BCD来求∠D的度数即可.
解:(1)直线EF与⊙O相切.理由如下:
如图,连接OE、OF.
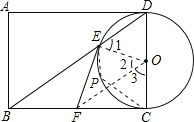
∵OD=OE,
∴∠1=∠D.
∵点F是BC的中点,点O是DC的中点,
∴OF∥BD,
∴∠3=∠D,∠2=∠1,
∴∠2=∠3.
∴在△EFO与△CFO中,
OE=OC,∠2=∠3,OF=OF,
∴△EFO≌△CFO(SAS),
∴∠FEO=∠FCO=90°,
∴直线EF与⊙O相切.
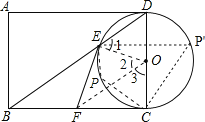
(2)如图,连接DF.
∵由(1)知,△EFO≌△CFO,
∴FC=EF=![]() .
.
∴BC=2![]()
在直角△FDC中,tan∠D=![]() =
=![]() ,
,
∴∠D=60°.
当点P在![]() 上时,
上时,
∵点E、P、C、D四点共圆,
∴∠EPC+∠D=180°,
∴∠EPC=120°.
当点P在 ![]() 上时,
上时,
∠EPC=∠D=60°,
故填:60°或120°.
“点睛”本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们知道,海拔高度每上升1 km,温度下降6 ℃.某时刻测量某市地面温度为20 ℃.设高出地面x km处的温度为y ℃,则y与x的函数关系式为___,y___x的一次函数(填“是”或“不是”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE,CF分别是AC,AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG. 
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意抛掷一枚骰子两次,骰子停止转动后,计算朝上的点数的和.
(1)和最小的是多少,和最大的是多少?
(2)下列事件:①点数的和为7;②点数的和为1;③点数的和为15.哪些是不可能性事件?哪些是不确定事件?
(3)点数的和为7与点数的和为2的可能性谁大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情境对话,然后解答问题

(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt![]() ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt
ABC 中, ∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt![]() ABC是奇异三角形,求a:b:c;
ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是上一点(不与点A、B重合),D是半圆的中点,CD在直径AB的两侧,若在⊙O内存在点E使得AE=AD,CB=CE.
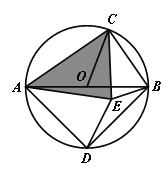
求证:![]() ACE是奇异三角形;
ACE是奇异三角形;
当![]() ACE是直角三角形时,求∠AOC的度数.
ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com