
【题目】如图,在平行四边形中,点O为对角线BD的中点,DE、BF分别平分∠ADC和∠ABC.
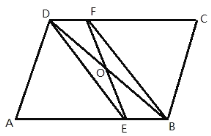
(1)求证:EF、BD互相平分;
(2)若∠A=60,AE=2EB,AD=4,求四边形DEBF的周长.
【答案】(1)见解析;(2)12.
【解析】
(1)根据平行四边形的对角相等以及角平分线的定义,证明∠ABF=∠AED,则DE∥BF,即可得到四边形DEBF是平行四边形,根据平行四边形的对角线互相平分即可证得;
(2)证明△ADE是等边三角形,求得AE、DE的长,则BE即可求得,进而求得DEBF的周长.
证明:(1)∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC.
又∵DE,BF分别是∠ADC,∠ABC的平分线,
∴∠ABF=∠CDE.
又∵∠CDE=∠AED,
∴∠ABF=∠AED,
∴DE∥BF,
∵DF∥BE
∴四边形DEBF是平行四边形,
∴EF,BD互相平分.
(2)由(1)知∠ADE=∠AED,
∵∠A=60°,
∴△ADE是等边三角形.
∴AE=DE=AD=4,
又∵AE:EB=2:1,
∴EB=2.
∴四边形DEBF的周长是12.


科目:初中数学 来源: 题型:
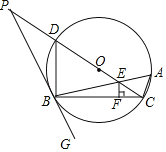
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而![]() =45是360°(多边形外角和)的
=45是360°(多边形外角和)的![]() ,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.

图2中的图案外轮廓周长是_____;
在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)解方程:|3x-2|-4=0.
(2)解关于x的方程:|x-2|=b+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形一边长为12cm,那么它的两条对角线的长度可以是( )
A. 8cm和14cm B. 10cm 和14cm C. 18cm和20cm D. 10cm和34cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论,其中,正确结论的个数是( )
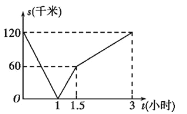
①出发1小时时,甲、乙在途中相遇;
②乙开车速度是80千米/小时;
③出发1.5小时时,乙比甲多行驶了60千米;
④出发3小时时,甲、乙同时到达终点;
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
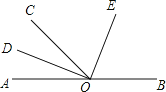
(1)请你数一数,图中有多少小于平角的角?
(2)求∠BOD的度数;
(3)试判断∠BOE和∠COE有怎样的数量关系,说说你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com