
【题目】在平行四边形ABCD中,AE平分![]() 交边BC于E,DF平分
交边BC于E,DF平分![]() 交边BC于F.若
交边BC于F.若![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】4或9
【解析】
首先根据题意画出图形,可知有两种形式,第一种为AE 与DF未相交,直接交于BC,第二种为AE与DF相交之后再交于BC.此时根据角平分线的定义和平行四边形的性质找到线段直接的关系.
(1)
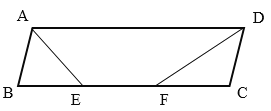
如图:∵AE平分∠BAD
∴∠BAE=∠DAE
又∵AD∥BC
∴∠DAE=∠BEA
即∠BEA=∠BEA
∴AB=BE
同理可得:DC=FC
又∵AB=DC
∴BE=CF
∵BC=AD=13,EF=5
∴BE=FC=(BC-EF)÷2=(13-5)÷2=4
即AB=BE=4
(2)
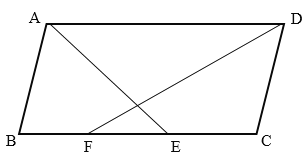
∵AE平分∠BAD
∴∠BAE=∠DAE
又∵AD∥BC
∴∠DAE=∠BEA
即∠BEA=∠BEA
∴AB=BE
同理可得:DC=FC
又∵AB=DC
∴BE=CF
则BE-EF=CE-EF
即BF=CE
而BC=AD=13,EF=5
∴BF=CE=(BC-EF)÷2=(13-5)÷2=4
∴BE=BF+EF=4+5=9
故AB=BE=9
综上所述:AB=4或9


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形中,点O为对角线BD的中点,DE、BF分别平分∠ADC和∠ABC.
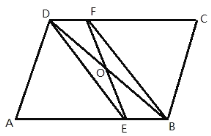
(1)求证:EF、BD互相平分;
(2)若∠A=60,AE=2EB,AD=4,求四边形DEBF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,∠A=∠C=90°.

(1)如图1,若BE平分∠ABC,DF平分∠ADC的邻补角,请写出BE与DF的位置关系,并证明.
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
(3)如图3,若BE、DE分别六等分∠ABC、∠ADC的邻补角(即∠CBE=![]() ∠CBM,∠CDE=
∠CBM,∠CDE=![]() ∠CDN),则∠E= .
∠CDN),则∠E= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是等腰Rt△ABC的外接圆,点D是![]() 上一点,BD交AC于点E,若BC=4,AD=
上一点,BD交AC于点E,若BC=4,AD=![]() ,则AE的长是( )
,则AE的长是( )
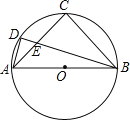
A. 1 B. 1.2 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 计算:
(1)解方程组:![]() ;
;
(2)解不等式组 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
(3)已知:(x+1)(x+2)-______=6x+2,请计算______内应填写的式子.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂一周计划每天生产200辆电动车,由于各种原因,实际每天的产量与计划相比有出入,下表是某周生产情况(超产为正,减产为负)
星期 | 一 | 二 | 三 | 四 | 五 |
增减 | +5 | -2 | -4 | +13 | -10 |
(1)产量最多一天是 辆,最少的一天是 辆.
(2)这一周一共生产了多少辆?
(3)该工厂按天计件计算工资,每生产一辆可得50元,若每超额一辆另奖15元,每少生产一辆另扣30元,那么该厂工人本周前三天的工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线经过点A(-3,0),点B(0,
中,直线经过点A(-3,0),点B(0,![]() ),点P的坐标为(1,0),与
),点P的坐标为(1,0),与![]() 轴相切于点O,若将⊙P沿
轴相切于点O,若将⊙P沿![]() 轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
轴向左平移,平移后得到(点P的对应点为点P′),当⊙P′与直线相交时,横坐标为整数的点P′共有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com