
【题目】(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
【答案】(1)每立方米的基本水价是2.45元,每立方米的污水处理费是1元;(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水15立方米
【解析】(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元,然后根据等量关系即可列出方程求出答案.
(2)设该用户7月份可用水t立方米(t>10),根据题意列出不等式即可求出答案.
(1)设每立方米的基本水价是x元,每立方米的污水处理费是y元
![]()
解得:![]()
答:每立方米的基本水价是2.45元,每立方米的污水处理费是1元.
(2)设该用户7月份可用水t立方米(t>10)
10×2.45+(t-10)×4.9+t≤64
解得:t≤15
答:如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水15立方米.


科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
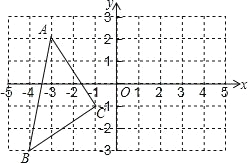
【题目】如图,在平面直角坐标系中,A(﹣3,2),B(﹣4,﹣3),C(﹣1,﹣1).
(1)在图中作出与△ABC 关于 y 轴对称的△A1B1C1(要求点 A 与 A1,点 B 与点B1,点 C 和点 C1 相对应);写出点 A1,B1,C1 的坐标(直接写答案)
(2)请求出△A1B1C1 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,C,D是直线AB上的两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.
(1)猜想:CE和DF是否平行?请说明理由;
(2)若∠DCE=130°,求∠DEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
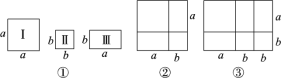
【题目】嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张.
问题发现
(1)他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②).根据图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是________________;
(2)如果要拼成一个长为a+2b,宽为a+b的大长方形,那么需要Ⅱ型卡片________张,Ⅲ型卡片________张.
拓展探究
(3)若a+b=5,ab=6,求a2+b2的值;
(4)当他拼成如图③所示的长方形时,根据图形的面积,可把多项式a2+3ab+2b2分解因式,其结果是________.
解决问题
(5)请你依照嘉嘉的方法,利用拼图分解因式:a2+5ab+6b2=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表: 甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图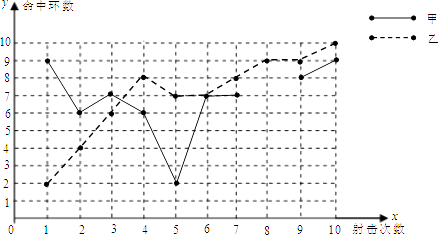
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学课上,刘老师请同学们心里想一个非零的有理数,然后把这个数按照下面的程序进行计算后,刘老师立刻说出计算结果.

(1)若小明同学心里想的数是8,请列出算式并计算最后的结果;
(2)小明又试了几个数进行计算,发现结果都相等,于是小明把心里想的这个数记作a(a≠0),并按照程序通过计算进行验证,请你写出这个验证过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com