
【题目】嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张.
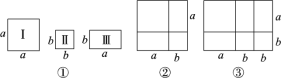
问题发现
(1)他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②).根据图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是________________;
(2)如果要拼成一个长为a+2b,宽为a+b的大长方形,那么需要Ⅱ型卡片________张,Ⅲ型卡片________张.
拓展探究
(3)若a+b=5,ab=6,求a2+b2的值;
(4)当他拼成如图③所示的长方形时,根据图形的面积,可把多项式a2+3ab+2b2分解因式,其结果是________.
解决问题
(5)请你依照嘉嘉的方法,利用拼图分解因式:a2+5ab+6b2=________.
【答案】(1)(a+b)2=a2+2ab+b2;(2)2,3;(3)13;(4)(a+2b)(a+b);(5)(a+2b)(a+3b)
【解析】
(1)利用图②的面积可得出这个乘法公式是(a+b)2=a2+2ab+b2;
(2)由如图③可得要拼成一个长为(a+2b),宽为(a+b)的大长方形所需要的Ⅱ型卡片、Ⅲ型卡片的数量;
(3)根据a2+b2= (a+b)2-2ab计算即可;
(4)由图③可知矩形面积为(a+2b)(a+b),利用面积得出a2+3ab+2b2=(a+2b)(a+b);
(5)先分解因式,再根据边长画图即可.
(1)这个乘法公式是(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2.
(2)由如图③可得要拼成一个长为(a+2b),宽为(a+b)的大长方形,则需要2号卡片2张,3号卡片3张.
故答案为:2,3.
(3)a2+b2= (a+b)2-2ab=25-2×6=25-12=13.
(4)由图③可知矩形面积为(a+2b)(a+b),所以a2+3ab+2b2=(a+2b)(a+b).
故答案为:(a+2b)(a+b).
(5)a2+5ab+6b2=(a+2b)(a+3b),如图:

故答案为:(a+2b)(a+3b).


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() .
.
其中正确的是(写出所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的内部点 A′的位置,试说明 2∠A=∠1+∠2;
(2)如图②,若把△ABC 纸片沿 DE 折叠,使点 A 落在四边形 BCED 的外部点A′的位置,写出∠A 与∠1、∠2 之间的等量关系(无需说明理由);
(3)如图③,若把四边形 ABCD 沿 EF 折叠,使点 A、D 落在四边形BCFE 的内部点 A′、D′的位置,请你探索此时∠A、∠D、∠1 与∠2 之间的数量关系,写出你发现的结论并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
X | 50 | 60 | 90 | 120 |
y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(列方程(组)及不等式解应用题)
水是人类生命之源.为了鼓励居民节约用水,相关部门实行居民生活用水阶梯式计量水价政策.若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,每立方米污水处理费不变.甲用户4月份用水8立方米,缴水费27.6元;乙用户4月份用水12立方米,缴水费46.3元.(注:污水处理的立方数=实际生活用水的立方数)
(1)求每立方米的基本水价和每立方米的污水处理费各是多少元?
(2)如果某用户7月份生活用水水费计划不超过64元,该用户7月份最多可用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论: ①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣ ![]() ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是(写出你认为正确的所有结论序号).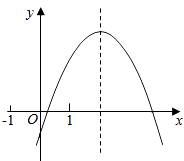
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com