
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论: ①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣ ![]() ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是(写出你认为正确的所有结论序号).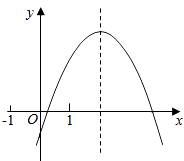
【答案】①③④
【解析】解:∵抛物线开口向下, ∴a<0,
∴2a<0,
对称轴x=﹣ ![]() >1,﹣b<2a,
>1,﹣b<2a,
∴2a+b>0,故选项①正确;
令ax2+bx+c=0,抛物线与轴交于(x1 , 0),(x2 , 0)则x1x2= ![]() ,
,
由图不能准确判断 ![]() 与1大小,则无法确定a,c的大小关系,故选项②不正确
与1大小,则无法确定a,c的大小关系,故选项②不正确
∵﹣1<m<n<1,则﹣2<m+n<2,
∴抛物线对称轴为:x=﹣ ![]() >1,
>1, ![]() >2,m+n
>2,m+n ![]() ,故选项③正确;
,故选项③正确;
当x=1时,a+b+c>0,2a+b>0,3a+2b+c>0,
∴3a+c>﹣2b,∴﹣3a﹣c<2b,
∵a<0,b>0,c<0(图象与y轴交于负半轴),
∴3|a|+|c|=﹣3a﹣c<2b=2|b|,故④选项正确.
所以答案是:①③④.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣1与反比例函数y= ![]() 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m). 
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC. 
(1)求证:BC平分∠PBD;
(2)求证:BC2=ABBD;
(3)若PA=6,PC=6 ![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉嘉同学动手剪了如图①所示的正方形与长方形纸片若干张.
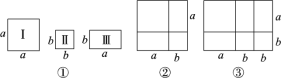
问题发现
(1)他用1张Ⅰ型、1张Ⅱ型和2张Ⅲ型卡片拼出一个新的图形(如图②).根据图形的面积关系写出一个你所熟悉的乘法公式,这个乘法公式是________________;
(2)如果要拼成一个长为a+2b,宽为a+b的大长方形,那么需要Ⅱ型卡片________张,Ⅲ型卡片________张.
拓展探究
(3)若a+b=5,ab=6,求a2+b2的值;
(4)当他拼成如图③所示的长方形时,根据图形的面积,可把多项式a2+3ab+2b2分解因式,其结果是________.
解决问题
(5)请你依照嘉嘉的方法,利用拼图分解因式:a2+5ab+6b2=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于点H,且DH与AC交于G,则GH=( ) 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表: 甲、乙射击成绩统计表
平均数 | 中位数 | 方差 | 命中10环的次数 | |
甲 | 7 | 0 | ||
乙 | 1 |
甲、乙射击成绩折线图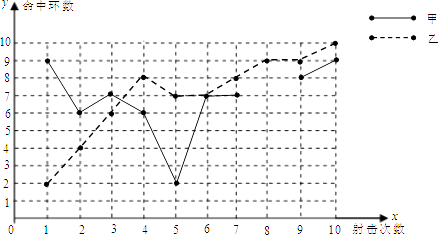
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P的度数为( )

A. 60° B. 70° C. 80° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△ECD都是等边三角形, B、C、D在一条直线上。
求证:(1)BE=AD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD;
(5)求∠EMD的度数。;
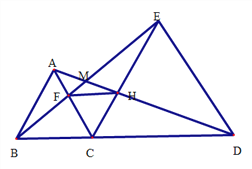
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( ) 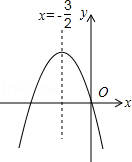
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com