
【题目】如图所示,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P的度数为( )

A. 60° B. 70° C. 80° D. 90°
科目:初中数学 来源: 题型:
【题目】(1)如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.

证明过程如下:
证明:过点E作EF∥AB,
∵AB∥DC,EF∥AB(辅助线的作法),
∴EF∥DC
∴∠C=∠CEF.
∵EF∥AB,∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC.
(2)如果点E运动到图②所示的位置,其他条件不变,∠B,∠C,∠BEC又有什么关系?并证明你的结论;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(写出结论,不用写计算过程)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
X | 50 | 60 | 90 | 120 |
y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论: ①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣ ![]() ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是(写出你认为正确的所有结论序号).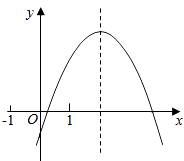
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D是边AC上一点,BC=BD=AD,则∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠1=∠2=∠3=∠4=24°,根据图形填空:
(1)是∠2的3倍的角是_________________(用字母表示)
(2)是∠AOD的![]() 的角有_________个;
的角有_________个;
(3)射线OC是哪个角的3等分线?又是哪个角的4等分线?
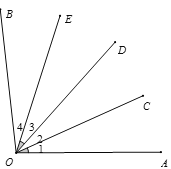
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com