
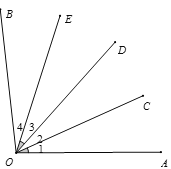
【题目】如图所示,∠1=∠2=∠3=∠4=24°,根据图形填空:
(1)是∠2的3倍的角是_________________(用字母表示)
(2)是∠AOD的![]() 的角有_________个;
的角有_________个;
(3)射线OC是哪个角的3等分线?又是哪个角的4等分线?
科目:初中数学 来源: 题型:
【题目】如图所示,BP是△ABC中∠ABC的平分线,CP是△ABC的外角∠ACM的平分线,如果∠ABP=20°,∠ACP=50°,那么∠A+∠P的度数为( )

A. 60° B. 70° C. 80° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是 . (写出所有正确说法的序号) ①当x=1.7时,[x]+(x)+[x)=6;
②当x=﹣2.1时,[x]+(x)+[x)=﹣7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( ) 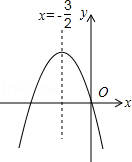
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,作射线AE,操作结果如图所示,下列结论不能由上述操作结果得出的是( ).
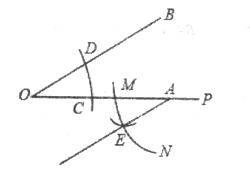
A. ∠ACD=∠EAP B. ∠ODC=∠AEM C. OB∥AE D. CD∥ME
查看答案和解析>>
科目:初中数学 来源: 题型:
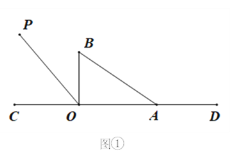
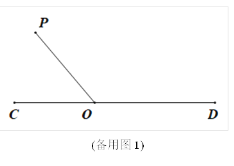
【题目】如图①,直线CD上有一点O,过点O在直线CD上方作射线OP.将一直角三角尺AOB(∠AOB=90°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线CD上方.将直角三角板绕着点O逆时针旋转.
(1)当直角三角板旋转到如图②的位置,OB恰好平分∠COP时,试证明:OA边恰好平分∠POD.
(2)若射线OP的位置保持不变,且∠COP=50°.当直角三角尺旋转到边AB与射线OC相交时则∠BOC与∠AOP有怎样的数量关系?试画出图形,写出数量关系,并写出说理过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式x2-4y2-2x+4y,细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式,过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法,利用这种方法解决下列问题:
(1)分解因式:a2-4a-b2+4;
(2)若△ABC三边a、b、c满足a2-ab-ac+bc=0,试判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,CD⊥AB于D,P是线段CD上一个动点,以P为直角顶点向下作等腰Rt△BPE,连结AE,DE.
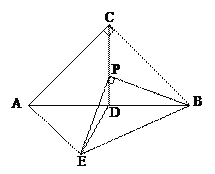
(1)∠BAE的度数是否为定值?若是,求出∠BAE的度数;
(2)直接写出DE的最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=2x+4的图象与x,y轴分别相交于点A,B,以AB为边作正方形ABCD(点D落在第四象限).
(1)求点A,B,D的坐标;
(2)联结OC,设正方形的边CD与x相交于点E,点M在x轴上,如果△ADE与△COM全等,求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com