
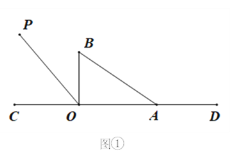
【题目】如图①,直线CD上有一点O,过点O在直线CD上方作射线OP.将一直角三角尺AOB(∠AOB=90°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线CD上方.将直角三角板绕着点O逆时针旋转.
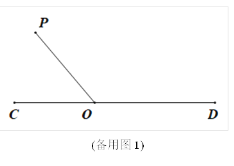
(1)当直角三角板旋转到如图②的位置,OB恰好平分∠COP时,试证明:OA边恰好平分∠POD.
(2)若射线OP的位置保持不变,且∠COP=50°.当直角三角尺旋转到边AB与射线OC相交时则∠BOC与∠AOP有怎样的数量关系?试画出图形,写出数量关系,并写出说理过程.

【答案】(1)见解析;(2)见解析.
【解析】
(1)根据角平分线的定义得到∠BOC=∠BOP ,再根据余角的定义可得∠AOD=∠AOP,根据角平分线的定义即可得到结论;
(2)分情况讨论:①当OA在∠POD内部或与OP重合,OB在CD下方时,②当OA在∠POC内部,OB在CD下方.
(1)∵OB恰好平分∠COP
∴∠BOC=∠BOP
又∵∠AOB=90°
∴∠AOD=180°-∠AOB-∠BOC
=180°-90°-∠BOC=90°-∠BOC
∠AOP=∠AOB-∠BOP=90°-∠BOP=90°-∠BOC
∴∠AOD=∠AOP
∴OA平分∠POD
(2)①如图,当OA在∠POD内部或与OP重合,OB在CD下方时,
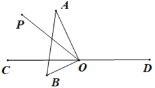
∠AOP+∠BOC=40
理由:∵∠AOB=90°,∠COP=50°
∴∠AOP+∠BOC=90°-∠POC=40°.
即:∠AOP+∠BOC=40°
②如图,当OA在∠POC内部,OB在CD下方时,
∠BOC-∠AOP=40°
理由:∵∠AOC=∠POC-∠AOP=50°-∠AOP
∠AOC=∠AOB-∠BOC=90°-∠BOC
∴50°-∠AOP=90°-∠BOC
∴∠BOC-∠AOP=40°
综上所述,当OA在∠POD内部或与OP重合,OB在CD下方时,
∠AOP+∠BOC=40°;当OA在∠POC内部,OB在CD下方时,
∠BOC-∠AOP=40°.


科目:初中数学 来源: 题型:
【题目】用A、B两种机器人搬运大米,A型机器人比B型机器人每小时多搬运20袋大米,A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等.求A、B型机器人每小时分别搬运多少袋大米.
查看答案和解析>>
科目:初中数学 来源: 题型:
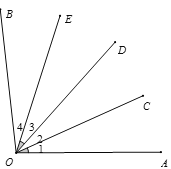
【题目】如图所示,∠1=∠2=∠3=∠4=24°,根据图形填空:
(1)是∠2的3倍的角是_________________(用字母表示)
(2)是∠AOD的![]() 的角有_________个;
的角有_________个;
(3)射线OC是哪个角的3等分线?又是哪个角的4等分线?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=40°,分别以AB,AC为边作两个等腰三角形ABD和ACE,且AB=AD,AC=AE,∠BAD=∠CAE=90°.

(1)求∠DBC的度数.
(2)求证:BD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
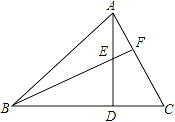
【题目】如图,在△ABC中,AD⊥BC于D,BF与AD相交于E.若AD=BD,BE=AC,BC=8cm,DC=3cm,则AE=_____,∠BFC=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com