
【题目】如图,△ABC内接于⊙O,∠CBG=∠A,CD为直径,OC与AB相交于点E,过点E作EF⊥BC,垂足为F,延长CD交GB的延长线于点P,连接BD.
(1)求证:PG与⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为8,PD=OD,求OE的长.
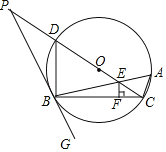
【答案】(1)证明见解析;(2)![]() ;(3)OE=2
;(3)OE=2![]() ﹣4.
﹣4.
【解析】
(1)要证PG与⊙O相切只需证明∠OBG=90°,由∠A与∠BDC是同弧所对圆周角且∠BDC=∠DBO可得∠CBG=∠DBO,结合∠DBO+∠OBC=90°即可得证;
(2)求![]() 需将BE与OC或OC相等线段放入两三角形中,通过相似求解可得,作OM⊥AC、连接OA,证△BEF∽△OAM得
需将BE与OC或OC相等线段放入两三角形中,通过相似求解可得,作OM⊥AC、连接OA,证△BEF∽△OAM得![]() ,由AM=
,由AM=![]() AC、OA=OC知
AC、OA=OC知![]() ,结合
,结合![]() 即可得;
即可得;
(3)Rt△DBC中求得BC=8![]() 、∠DCB=30°,在Rt△EFC中设EF=x,知EC=2x、FC=
、∠DCB=30°,在Rt△EFC中设EF=x,知EC=2x、FC=![]() x、BF=8
x、BF=8![]() ﹣
﹣![]() x,继而在Rt△BEF中利用勾股定理求出x的,从而得出答案.
x,继而在Rt△BEF中利用勾股定理求出x的,从而得出答案.
(1)如图,连接OB,则OB=OD,
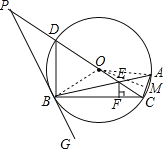
∴∠BDC=∠DBO,
∵∠BAC=∠BDC、∠BDC=∠GBC,
∴∠GBC=∠BDC,
∵CD是⊙O的切线,
∴∠DBO+∠OBC=90°,
∴∠GBC+∠OBC=90°,
∴∠GBO=90°,
∴PG与⊙O相切;
(2)过点O作OM⊥AC于点M,连接OA,
则∠AOM=∠COM=![]() ∠AOC,
∠AOC,
∵![]() ,
,
∴∠ABC=![]() ∠AOC,
∠AOC,
又∵∠EFB=∠OGA=90°,
∴△BEF∽△OAM,
∴![]() ,
,
∵AM=![]() AC,OA=OC,
AC,OA=OC,
∴![]() ,
,
又∵![]() ,
,
∴![]() ;
;
(3)∵PD=OD,∠PBO=90°,
∴BD=OD=8,
在Rt△DBC中,BC=![]() =8
=8![]() ,
,
又∵OD=OB,
∴△DOB是等边三角形,
∴∠DOB=60°,
∵∠DOB=∠OBC+∠OCB,OB=OC,
∴∠OCB=30°,
∴![]() ,
,![]() =
=![]() ,
,
∴可设EF=x,则EC=2x、FC=![]() x,
x,
∴BF=8![]() ﹣
﹣![]() x,
x,
在Rt△BEF中,BE2=EF2+BF2,
∴100=x2+(8![]() ﹣
﹣![]() x)2,
x)2,
解得:x=6±![]() ,
,
∵6+![]() >8,舍去,
>8,舍去,
∴x=6﹣![]() ,
,
∴EC=12﹣2![]() ,
,
∴OE=8﹣(12﹣2![]() )=2
)=2![]() ﹣4.
﹣4.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】将连续的奇数1,3,5,7,9……排成如下的数表:
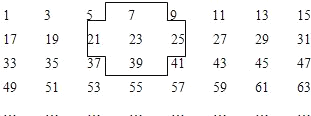
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为![]() ,用含
,用含![]() 的式子表示十字框中的其他四个数;
的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2019吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线相交于点A1,得∠A1;∠A1BC和∠A1CD的平分线相交于点A2,得∠A2;…;∠A2018BC和∠A2018CD的平分线交于点A2019,则∠A2019=________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”,
(1)如图△ABC中,AB=AC=![]() ,BC=2,求证:△ABC是“美丽三角形”;
,BC=2,求证:△ABC是“美丽三角形”;
(2)在Rt△ABC中,∠C=90°,AC=2![]() ,若△ABC是“美丽三角形”,求BC的长.
,若△ABC是“美丽三角形”,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
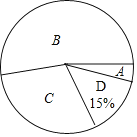
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
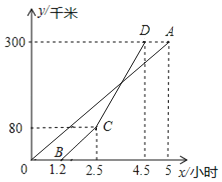
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地![]() 轿车的平均速度大于货车的平均速度
轿车的平均速度大于货车的平均速度![]() ,如图,线段OA、折线BCD分别表示两车离甲地的距离
,如图,线段OA、折线BCD分别表示两车离甲地的距离![]() 单位:千米
单位:千米![]() 与时间
与时间![]() 单位:小时
单位:小时![]() 之间的函数关系.
之间的函数关系.
![]() 线段OA与折线BCD中,______表示货车离甲地的距离y与时间x之间的函数关系.
线段OA与折线BCD中,______表示货车离甲地的距离y与时间x之间的函数关系.
![]() 求线段CD的函数关系式;
求线段CD的函数关系式;
![]() 货车出发多长时间两车相遇?
货车出发多长时间两车相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形中,点O为对角线BD的中点,DE、BF分别平分∠ADC和∠ABC.
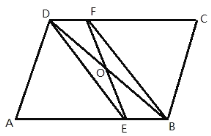
(1)求证:EF、BD互相平分;
(2)若∠A=60,AE=2EB,AD=4,求四边形DEBF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com