【题目】如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“美丽三角形”，

(1)如图△ABC中，AB=AC=，BC=2，求证：△ABC是“美丽三角形”；

(2)在Rt△ABC中，∠C=90°，AC=2，若△ABC是“美丽三角形”，求BC的长．

参考答案：

【答案】（1）见解析；（2）BC=3或BC=4.

【解析】

（1）由“美丽三角形”的定义知，要求出△ABC的中线长，再作比较，由AB=AC=，可知△ABC是等腰三角形，由“三线合一”，可作BC的中线AD,则AD即为BC的高线，由勾股定理求AD的长即可证明；

（2）Rt△ABC中有三条中线，由斜边上的中线是斜边的一半，排除斜边的中线；则有两种可能：AC边的中线等于AC或BC边的中线等于BC.结合中线的定义及勾股定理即可解答.

（1）证明：如图，作BC的中线AD，如图，

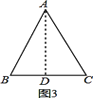
∵AB=AC= ，AD是BC的中线，

∴AD⊥BC, BD=CD= ,

在Rt△ABD中，由勾股定理得AD= ,

∴AD=BC，

∴△ABC是美丽三角形.

（2）解：①如图1，作AC的中线BD，△ABC是“美丽三角形”，

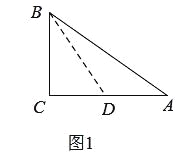
当BD=AC= 时，

则CD= ,

由勾股定理得 .

②如图2，作BC的中线AD，△ABC是“美丽三角形”，

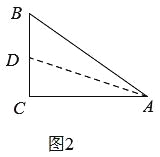
当BC=AD时，

则CD= ,

在Rt△ACD中，由勾股定理得 ，

则 ，解得CD=2，

∴BC=2CD=4.

故BC=3或BC=4.

关闭