
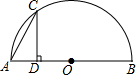
 如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )
如图,点C是以点O为圆心、AB为直径的半圆上的一个动点(点C不与点A、B重合),如果AB=4,过点C作CD⊥AB于D,设弦AC的长为x,线段CD的长为y,那么在下列图象中,能表示y与x函数关系的图象大致是( )| A. | 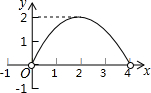 | B. | 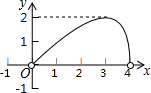 | ||
| C. | 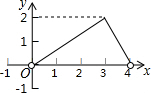 | D. | 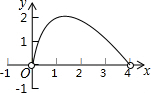 |
分析 连结BC,如图,根据圆周角定理得到∠ACB=90°,则利用勾股定理得到BC=$\sqrt{16-{x}^{2}}$,再利用面积法可得到y=$\frac{x•\sqrt{16-{x}^{2}}}{4}$,CD为半径时最大,即y的最大值为2,此时x=2$\sqrt{2}$,由于y与x函数关系的图象不是抛物线,也不是一次函数图象,则可判断A、C错误;利用y最大时,x=2$\sqrt{2}$可对B、D进行判断.
解答 解:连结BC,如图,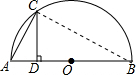
∵AB为直径,
∴∠ACB=90°,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{16-{x}^{2}}$,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴y=$\frac{x•\sqrt{16-{x}^{2}}}{4}$,
∵y的最大值为2,此时x=2$\sqrt{2}$.
故选B.
点评 本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.解决本题的关键是利用圆周角定理得到∠ACB=90°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图,点C在线段AB上,线段AC=6cm,BC=10cm,点D、E分别是AC和BC的中点.求线段DE的长;
(1)如图,点C在线段AB上,线段AC=6cm,BC=10cm,点D、E分别是AC和BC的中点.求线段DE的长;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20000(1+x)2=80000 | B. | 20000(1+x)+20000(1+x)2=80000 | ||
| C. | 20000(1+x2)=80000 | D. | 20000+20000(1+x)+20000(1+x)2=80000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | … | 0.04 | 4 | 400 | 40000 | … |
| $\sqrt{a}$ | … | x | 2 | y | z | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com