
如图所示,在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角a(0°<a<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点。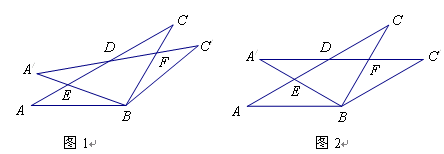
(1)如图1,观察并猜想,在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论;
(2)如图2,当a=30°时,试判断四边形BC1DA的形状,并说明理由;
(3)在(2)的情况下,求ED的长。
(1)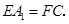 (2)四边形
(2)四边形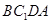 是菱形.(3)ED
是菱形.(3)ED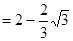
解析试题分析:(1)根据等边对等角及旋转的特征可得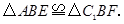 即可证得结论;
即可证得结论;
(2)先根据两组对边分别平行的四边形是平行四边形,再得到邻边相等即可判断结论;
(3)过点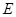 作
作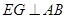 于点
于点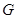 ,解
,解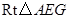 可得AE的长,结合菱形的性质即可求得结果。
可得AE的长,结合菱形的性质即可求得结果。
(1)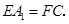
证明:(证法一)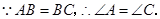
由旋转可知,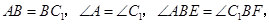
∴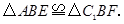
∴ 又
又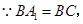
∴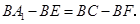 即
即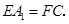
(证法二)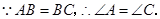
由旋转可知,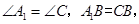 而
而
∴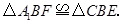
∴ ∴
∴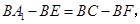
即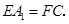
(2)四边形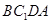 是菱形.
是菱形.
证明: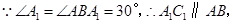 同理
同理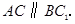
∴四边形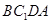 是平行四边形.
是平行四边形.
又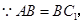 ∴四边形
∴四边形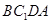 是菱形.
是菱形.
(3)过点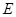 作
作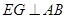 于点
于点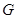 ,则
,则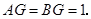

在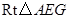 中,
中,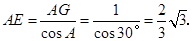
由(2)知四边形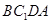 是菱形,
是菱形,
∴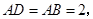
∴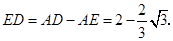
考点:本题考查的是旋转的性质,菱形的判定与性质,解直角三角形
点评:解答本题的关键是掌握好旋转的性质,平行四边形判定与性质,的菱形的判定与性质,选择适当的条件解决问题。


科目:初中数学 来源: 题型:
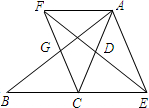 如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.
如图所示,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作AF∥BC交ED的延长线于点F,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:
 15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=
15、如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E,若∠DAE=50°,则∠BAC=查看答案和解析>>
科目:初中数学 来源: 题型:
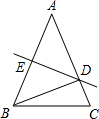 如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为
如图所示,在△ABC中,AB=AC,DE是边AB的垂直平分线,交AB于E,交AC于D,若△BCD的周长为18cm,△ABC的周长为30cm,那么BE的长为查看答案和解析>>
科目:初中数学 来源: 题型:
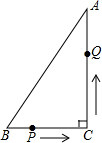 如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.
如图所示,在△ABC中,BC=7cm,AB=25cm,AC=24cm,P点在BC上从B点向C点运动(不包括点C),点P的运动速度为2cm∕s;Q点在AC上从C点向点A运动(不包括点A),运动速度为5cm∕s,若点P、Q分别从B、C同时运动,请解答下面的问题,并写出主要过程.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com