
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��a��0����B��n��0����a��n����|a+2|+![]() =0����ͬʱ����A��B�ֱ�����ƽ��4����λ��������ƽ��3����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD��
=0����ͬʱ����A��B�ֱ�����ƽ��4����λ��������ƽ��3����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD��
��1�����C��D�����꼰�ı���OBDC�������
��2����ͼ2���� ��P���߶�BD�ϵ�һ�����㣬����PC��PO������P��BD���ƶ�ʱ������B��D�غϣ�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
��3�����ı���OBDC���Ƿ����һ��P������PO��PB��PC��PD��ʹS��PCD=S��PBD�� S��POB��S��POC=1������������һ�㣬�����P�����꣬�������ڣ���˵�����ɣ�

���𰸡���1��24��2����ֵ���䣬1��3�����ڣ�P��3��2��
��������
��1�����ݱ��������;���ֵ���ڵ���0��ʽ���b��n���Ӷ��õ�A��B�����꣬�ٸ�������ƽ��4����λ�����������4������ƽ��3����λ����������3�������C��D�����꼴�ɣ�Ȼ������ƽ���ı��ε������ʽ����ʽ���㣻
��2������ƽ�Ƶ����ʿɵ�AB��CD���ٹ���P��PE��AB������ƽ�й����ɵ�PE��CD��Ȼ�������ֱ��ƽ�У��ڴ�����ȿɵá�DCP=��CPE����BOP=��OPE��Ȼ�������CPO=��DCP+��BOP���Ӷ��жϳ���ֵ���䣻
��3�����������ȵ������Կ�֪����PΪƽ���ı���ABCD�Խ��ߵĽ��㣬��PB=PC����˸����е�������P�����꣮
��1����ͼ1��
������ã�a+2=0��a=��2����A����2��0����
5��n=0��n=5����B��5��0����
�ߵ�A��B�ֱ�����ƽ��4����λ��������ƽ��3����λ��
���C��1��4����D��8��4����
��OB=5��CD=8��1=7��
��S�ı���OBDC=![]() ��CD+OB����h=
��CD+OB����h=![]() ��4����5+7��=24��
��4����5+7��=24��
��2��![]() ��ֵ�������仯����ֵΪ1�������ǣ�
��ֵ�������仯����ֵΪ1�������ǣ�
��ƽ�Ƶ����ʿɵ�AB��CD��
��ͼ2������P��PE��AB����AC��E����PE��CD��
���DCP=��CPE����BOP=��OPE��
���CPO=��CPE+��OPE=��DCP+��BOP��
��![]() =1����ֵ������
=1����ֵ������
��3�����ڣ���ͼ3������AD��BC���ڵ�P��
��AB=CD��AB��CD��
���ı���ABCD��ƽ���ı��Σ�
��BP=CP��
��S��PCD=S��PBD�� S��POB��S��POC=1��
��C��1��4����B��5��0��
��P��3��2����


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼���ѧ���Ŀ�ҵ������ij�н����������Ź涨��ѧ��ÿ����ɼ�ͥ��ҵ��ƽ��ʱ�䲻�ܳ���1.5Сʱ��Ϊ���˽������ѧ����ҵ����������Բ���ѧ��ÿ����ɼ�ͥ��ҵ���õ�ʱ������˳������飬�������������Ƴ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
��1������ε����й������˶�����ѧ����
��2���ֱ����ÿ����ɼ�ͥ��ҵ���õ�ʱ��Ϊ��1Сʱ���͡�2Сʱ����ѧ������ռ�������İٷֱȣ��Լ����õ�ʱ��Ϊ��1.5Сʱ����ѧ������������ȫ����ͳ��ͼ��
��3�����ε����У���ѧ��ÿ����ɼ�ͥ��ҵ���õ�ƽ��ʱ���Ƿ����Ҫ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У���B=90�㣬AB=3��BC=4��CD=12��AD=13�����ı���ABCD�������
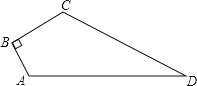
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016����ʡ�����У�ij�жԳ����ۺ����ʲ����е��������������п��ˣ��涨���£������ۺ����۵÷��ɲ��Գɼ�������100�֣���ƽʱ�ɼ�������100�֣���������ɣ����в��Գɼ�ռ80%��ƽʱ�ɼ�ռ20%�����ҵ��ۺ����۵÷ִ��ڻ����80��ʱ�������ۺ�����ΪA�ȣ�
��1������ͬѧ�IJ��Գɼ���ƽʱ�ɼ�����÷�֮��Ϊ185�֣����ۺ����۵÷�Ϊ91�֣������ͬѧ���Գɼ���ƽʱ�ɼ����ö��ٷ֣�
��2��ijͬѧ���Գɼ�Ϊ70�֣������ۺ����۵÷��п��ܴﵽA����Ϊʲô��
��3�����һ��ͬѧ�ۺ�����Ҫ�ﵽA�ȣ����IJ��Գɼ�����Ҫ���ٷ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC ��AD = 9cm��BC = 6cm����P��Q�ֱ�ӵ�A��Cͬʱ��������P��1cm/s���ٶ���A��D�˶�����Q��2cm/s���ٶ���C��B�˶����ʼ����ֱ��PQ���ı���ABCD�س�һ��ƽ���ı��Σ�
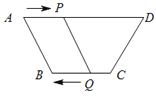
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ABC��λ����ͼ��ʾ��ÿ��С�����DZ߳�Ϊ1����λ���ȵ������Σ���
��1������ABC��x�᷽������ƽ��6����λ������ƽ�ƺ�õ��ġ�A1B1C1��
��2������ABC���ŵ�A˳ʱ����ת90�㣬������ת��õ��ġ�AB2C2����ֱ��д����B2��C2�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������Ϊ4�ĵ���ֱ�������η���ֱ������ϵ�У�˳�����Ӹ����е�õ���1�������Σ���˳�����Ӹ����е�õ���2����������������˲�����ȥ����ô����6�������ε�ֱ�Ƕ�������Ϊ��������

A. ����![]() ��
��![]() �� B. ����
�� B. ����![]() ��
��![]() �� C. ����
�� C. ����![]() ��
��![]() �� D. ����
�� D. ����![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
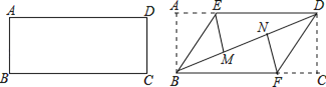
����Ŀ����һ�ž���ֽƬ������ͼ����������ABE��BE���ۣ�ʹ��A���ڶԽ���BD�ϵ�M�㣬����CDF��DF���ۣ�ʹ��C���ڶԽ���BD�ϵ�N�㣮
��1����֤���ı���BFDE��ƽ���ı���.
��2�����ı���BFDE�����Σ�BE =2��������BFDE�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com