
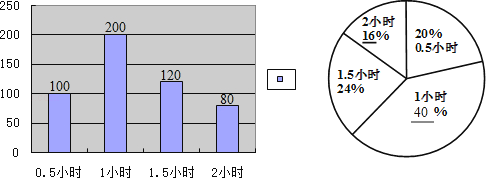
【题目】为了减轻学生的课业负担,某市教育行政部门规定中学生每天完成家庭作业的平均时间不能超过1.5小时,为了了解该市中学生课业负担情况,对部分学生每天完成家庭作业所用的时间进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)分别求出每天完成家庭作业所用的时间为“1小时”和“2小时”的学生人数占总人数的百分比,以及所用的时间为“1.5小时”的学生人数,并补全两个统计图;
(3)本次调查中,中学生每天完成家庭作业所用的平均时间是否符合要求?并说明理由.
【答案】
(1)
解:根据题意得:100÷20%=500(人),
则调查的学生数为500人;
(2)
解:每天完成家庭作业的时间为为1小时的人数为200人,占的百分比为 ![]() ×100%=40%;
×100%=40%;
每天完成家庭作业的时间为1.5小时的学生数为500×24%=120(人);
每天完成家庭作业的时间为2小时的学生数为500×16%=80(人),
补全统计图,如图所示:
(3)
解:符合要求,理由为:调查学生每天完成家庭作业的平均时间为0.5×20%+1×40%+1.5×24%+2×16%=0.1+0.4+0.36+0.32=1.18(小时)<1.5小时,则本次调查中,中学生每天完成家庭作业所用的平均时间符合要求.
【解析】(1)根据每天完成家庭作业的时间为0.5小时的人数除以所占的百分比即可确定出共调查的学生数;(2)由学生总数求出每天完成家庭作业的时间为1.5小时的学生数,补全条形统计图,求出每天完成家庭作业的时间为1小时的学生数占的百分比,补全扇形统计图即可;(3)求出调查学生每天完成家庭作业的平均时间,比较即可得到结果.
【考点精析】关于本题考查的扇形统计图和条形统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】为了提高沈城市民的节水意识,有关部门就“你认为最有效的节水措施”随机对部分市民进行了问卷调查,其中问卷设置以下选项(被调查者只能选择其中的一项)A.出台相关法律法规 B.控制用水大户数量 C.推广节水技改和节水器具 D.用水量越多,水价越高. E.其他
根据调查结果制作了统计图表的一部分如下: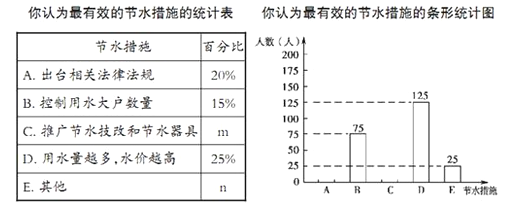
(1)此次抽样调查的人数为人;
(2)结合上述统计图表可得m=;n= .
(3)请根据以上信息直接补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要同时运输A、B两种型号的商品共13件,A型商品每件体积为2m3 , 每件质量为1吨;B型商品每件体积为0.8m3 , 每件质量为0.5吨,这两种型号商品体积之和不超过18.8m3 , 质量之和大于8.5吨.
(1)求A、B两种型号商品的件数共有几种可能?写出所有可能情况;
(2)若一件A型商品运费为200元,一件B型商品运费为180元.则(1)中哪种情况的运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的![]() ;
;
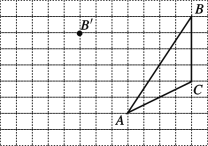
(2)画出![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_________;
的面积为_________;
(5)在图中能使![]() 的格点
的格点![]() 的个数有________个(点
的个数有________个(点![]() 异于点
异于点![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为4000元的电视以4400元售出,平均每天能售出6台.为了配合国家财政推出的“节能家电补贴政策”的实施,商场决定采取适当的降价措施,调查发现:这种电视的售价每降价50元,平均每天就能多售出3台.
(1)现设每台电视降价x元,商场每天销售这种电视的利润是y元,请写出y与x之间的函数表达式.(不要求写出自变量的取值范围)
(2)每台电视降价多少元时,商场每天销售这种电视的利润最高?最高利润是多少?
(3)商场要想在这种电视销售中每天盈利3600元,同时又要使百姓得到更多实惠,每台电视应降价多少元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于3600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC的两边分别平行于∠DEF的两条边,且∠ABC=45°.
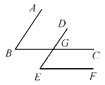
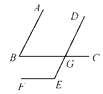
图1 图2
(1)图1中:∠DEF=_________,图2中:∠DEF=_________;
(2)请观察图1、图2中∠DEF分别与∠ABC有怎样的关系,请你归纳出一个命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(n,0)且a、n满足|a+2|+![]() =0,现同时将点A,B分别向上平移4个单位,再向右平移3个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
=0,现同时将点A,B分别向上平移4个单位,再向右平移3个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形OBDC的面积;
(2)如图2,若 点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
(3)在四边形OBDC内是否存在一点P,连接PO,PB,PC,PD,使S△PCD=S△PBD; S△POB:S△POC=1?若存在这样一点,求出点P的坐标,若不存在,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com