
【题目】某商场将进价为4000元的电视以4400元售出,平均每天能售出6台.为了配合国家财政推出的“节能家电补贴政策”的实施,商场决定采取适当的降价措施,调查发现:这种电视的售价每降价50元,平均每天就能多售出3台.
(1)现设每台电视降价x元,商场每天销售这种电视的利润是y元,请写出y与x之间的函数表达式.(不要求写出自变量的取值范围)
(2)每台电视降价多少元时,商场每天销售这种电视的利润最高?最高利润是多少?
(3)商场要想在这种电视销售中每天盈利3600元,同时又要使百姓得到更多实惠,每台电视应降价多少元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于3600元?
【答案】
(1)
解:设每台电视降价x元,商场每天销售这种电视的利润是y元,
根据题意得出:y=(6+ ![]() ×3)(4400﹣4000﹣x)=﹣
×3)(4400﹣4000﹣x)=﹣ ![]() x2+18x+2400
x2+18x+2400
(2)
解:∵y=﹣ ![]() x2+18x+2400=﹣
x2+18x+2400=﹣ ![]() (x﹣150)2+3750,
(x﹣150)2+3750,
∴当x=150元时,y最大=3750元;
答:每台电视降价150元时,商场每天销售这种电视的利润最高,最高利润是3750元
(3)
解:∵商场要想在这种电视销售中每天盈利3600元,
∴3600=﹣ ![]() (x﹣150)2+3750,
(x﹣150)2+3750,
解得:x1=200,x2=100,
∵要使百姓得到更多实惠,
∴每台电视应降价200元,
∴售价在4200元到4300元范围时,每个月的利润不低于3600元
【解析】(1)根据销量乘以每台利润=总利润,进而得出y与x之间的函数表达式;(2)利用配方法求出二次函数最值即可;(3)利用(1)中所求解析式以及一元二次方程的解法得出x的值,进而利用二次函数增减性得出答案.


科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1 , l2的表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示)
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.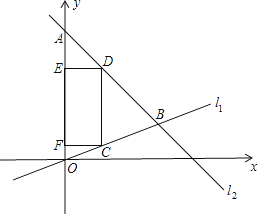
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据2013﹣2017年某市财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
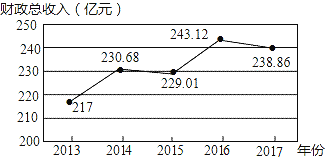
A. 2013~2017年财政总收入呈逐年增长
B. 预计2018年的财政总收入约为253.43亿元
C. 2014~2015年与2016~2017年的财政总收入下降率相同
D. 2013~2014年的财政总收入增长率约为6.3%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减轻学生的课业负担,某市教育行政部门规定中学生每天完成家庭作业的平均时间不能超过1.5小时,为了了解该市中学生课业负担情况,对部分学生每天完成家庭作业所用的时间进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)分别求出每天完成家庭作业所用的时间为“1小时”和“2小时”的学生人数占总人数的百分比,以及所用的时间为“1.5小时”的学生人数,并补全两个统计图;
(3)本次调查中,中学生每天完成家庭作业所用的平均时间是否符合要求?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有理数的原有运算法则中,我们补充定义一种新运算“★”如下:a★b=(a+b)(a﹣b),例如:5★3=(5+3)×(5﹣3)=8×2=16,下面给出了关于这种新运算的几个结论:① 3★(﹣2)=5;②a★b=b★a;③若b=0,则a★b=a2;④若a★b=0,则a=b.其中正确结论的有__;(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com