
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1 , l2的表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示)
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.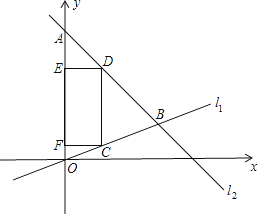
【答案】
(1)
解:设直线l1的表达式为y=k1x,它过(18,6)得18k1=6 k1= ![]()
∴y= ![]() x
x
设直线l2的表达式为y=k2x+b,它过点A(0,24),B(18,6)
得 ![]() 解得
解得 ![]() ,
,
∴直线l2的表达式为:y=﹣x+24;
(2)
解:①∵点C在直线l1上,且点C的纵坐标为a,
∴a= ![]() x x=3a,
x x=3a,
∴点C的坐标为(3a,a),
∵CD∥y轴
∴点D的横坐标为3a,
∵点D在直线l2上,
∴y=﹣3a+24
∴D(3a,﹣3a+24)
②∵C(3a,a),D(3a,﹣3a+24)
∴CF=3a,CD=﹣3a+24﹣a=﹣4a+24,
∵矩形CDEF的面积为60,
∴S矩形CDEF=CFCD=3a×(﹣4a+24)=60,解得a=1或a=5,
当a=1时,3a=3,故C(3,1);
当a=5时,3a=15,故C(15,5);
综上所述C点坐标为:C(3,1)或(15,5).
【解析】(1)设直线l1的表达式为y=k1x,它过(18,6)可求出k1的值,进而得出其解析式;设直线l2的表达式为
y=k2x+b,由于它过点A(0,24),B(18,6),故把此两点坐标代入即可求出k2 , b的值,进而得出其解析式;(2)①因为点C在直线l1上,且点C的纵坐标为a,故把y=a代入直线l1的表达式即可得出x的值,进而得出C点坐标,由于CD∥y轴,所以点D的横坐标为3a,再根据点D在直线l2上即可得出点D的纵坐标,进而得出结论;
②先根据CD两点的坐标用a表示出CF及CD的值,由矩形的面积为60即可求出a的值,进而得出C点坐标.
【考点精析】关于本题考查的一次函数的性质和一次函数的图象和性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:如图1,平面直角坐标系xOy中,四边形OABC是矩形,点A,C的坐标分别为(6,0),(0,2).点D是线段BC上的一个动点(点D与点B,C不重合),过点D作直线y=-![]() x+b交折线O-A-B于点E.
x+b交折线O-A-B于点E.
(1)在点D运动的过程中,若△ODE的面积为S,求S与b的函数关系式,并写出自变量的取值范围;
(2)如图2,当点E在线段OA上时,矩形OABC关于直线DE对称的图形为矩形O′A′B′C′,C′B′分别交CB,OA于点D,M,O′A′分别交CB,OA于点N,E.求证:四边形DMEN是菱形;
(3)问题(2)中的四边形DMEN中,ME的长为____________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1计算:![]() ;
;
(2)解不等式组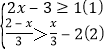
请结合题意填空,完成本题的解答:
解不等式(1),得______________.
解不等式(2),得_______________.
把不等式(1)和(2)的解集在数轴上表示出来
![]()
∴原不等式组的解集为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高沈城市民的节水意识,有关部门就“你认为最有效的节水措施”随机对部分市民进行了问卷调查,其中问卷设置以下选项(被调查者只能选择其中的一项)A.出台相关法律法规 B.控制用水大户数量 C.推广节水技改和节水器具 D.用水量越多,水价越高. E.其他
根据调查结果制作了统计图表的一部分如下: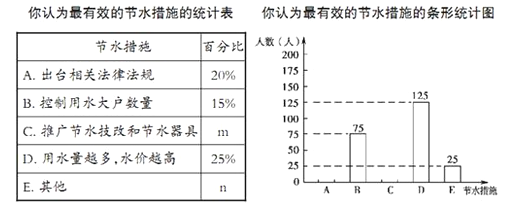
(1)此次抽样调查的人数为人;
(2)结合上述统计图表可得m=;n= .
(3)请根据以上信息直接补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有如图所示的一块地,已知AD=4米,CD=3米,![]() ,AB=13米,BC=12米.
,AB=13米,BC=12米.
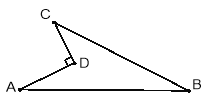
(1)试判断以点A、点B、点C为顶点的三角形是什么三角形?并说明理由.
(2)求这块地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠3=∠B,∠4=65°,求证∠ACB=∠4.请填空完
成证明过程:
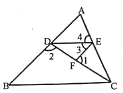
∵∠1+∠2=180°(______________)∠1+∠______=180°
∴∠2=∠DFE(___________________)
∴AB∥EF(____________________)
∴∠3=∠ADE(____________)
又∵∠3=∠B
∴∠ADE=∠_______
∴DE∥BC(____________)
∴∠ACB=∠4(_______________)
∴∠ACB=65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为4000元的电视以4400元售出,平均每天能售出6台.为了配合国家财政推出的“节能家电补贴政策”的实施,商场决定采取适当的降价措施,调查发现:这种电视的售价每降价50元,平均每天就能多售出3台.
(1)现设每台电视降价x元,商场每天销售这种电视的利润是y元,请写出y与x之间的函数表达式.(不要求写出自变量的取值范围)
(2)每台电视降价多少元时,商场每天销售这种电视的利润最高?最高利润是多少?
(3)商场要想在这种电视销售中每天盈利3600元,同时又要使百姓得到更多实惠,每台电视应降价多少元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于3600元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com