
【题目】如图,已知∠1+∠2=180°,∠3=∠B,∠4=65°,求证∠ACB=∠4.请填空完
成证明过程:
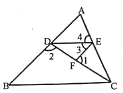
∵∠1+∠2=180°(______________)∠1+∠______=180°
∴∠2=∠DFE(___________________)
∴AB∥EF(____________________)
∴∠3=∠ADE(____________)
又∵∠3=∠B
∴∠ADE=∠_______
∴DE∥BC(____________)
∴∠ACB=∠4(_______________)
∴∠ACB=65°
【答案】已知;DFE;同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;B;同位角相等,两直线平行;两直线平行,同位角相等.
【解析】
求出∠2=∠DFE,根据平行线的判定得出AB∥EF,根据平行线的性质得出∠3=∠ADE,求出∠B=∠ADE,根据平行线的判定得出DE∥BC,即可得出答案.
证明:
∵∠1+∠2=180° (已知),∠1+∠DFE=180°,
∴∠2=∠DFE (同角的补角相等),
∴AB∥EF (内错角相等,两直线平行),
∴∠3=∠ADE (两直线平行,内错角相等),
又∵∠3=∠B,
∴∠ADE=∠B,
∴DE∥BC (同位角相等,两直线平行),
∴∠ACB=∠4 (两直线平行,同位角相等),
∴∠ACB=65°,


科目:初中数学 来源: 题型:
【题目】如图,把一个棱长为![]() 的正方体的每个面等分成
的正方体的每个面等分成![]() 个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去
个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去![]() 个小正方体),所得到的几何体的表面积是( )
个小正方体),所得到的几何体的表面积是( )

A. 78 B. 72 C. 54 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b)且a、b满足![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.
(1)点B的坐标为_______;当点P移动3.5秒时,点P的坐标为__________;
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
(1)求直线l1 , l2的表达式;
(2)点C为线段OB上一动点(点C不与点O,B重合),作CD∥y轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
①设点C的纵坐标为a,求点D的坐标(用含a的代数式表示)
②若矩形CDEF的面积为60,请直接写出此时点C的坐标.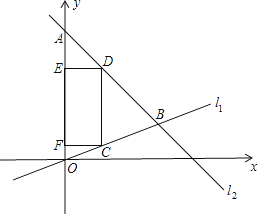
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图1的调查问卷(单选),在随机调查了本市10000名司机中的部分司机后,统计整理并制作了如图2所示的统计图: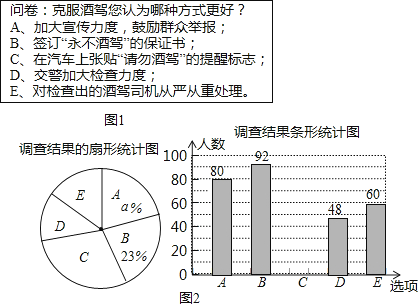
根据以上的信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中a= .
(2)该市支持选项C的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据2013﹣2017年某市财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
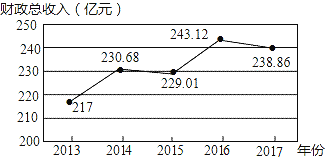
A. 2013~2017年财政总收入呈逐年增长
B. 预计2018年的财政总收入约为253.43亿元
C. 2014~2015年与2016~2017年的财政总收入下降率相同
D. 2013~2014年的财政总收入增长率约为6.3%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学阅读:
古希腊数学家海伦曾提出一个利用三角形三边之长求面积的公式:若一个三角形的三边长分别为a、b、c,则这个三角形的面积为![]() ,其中
,其中![]() .这个公式称为“海伦公式”.
.这个公式称为“海伦公式”.
数学应用:
如图1,在△ABC中,已知AB=9,AC=8,BC=7.
(1)请运用海伦公式求△ABC的面积;
(2)设AB边上的高为![]() ,AC边上的高
,AC边上的高![]() ,求
,求![]() 的值;
的值;
(3)如图2,AD、BE为△ABC的两条角平分线,它们的交点为I,求△ABI的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com