
【题目】在有理数的原有运算法则中,我们补充定义一种新运算“★”如下:a★b=(a+b)(a﹣b),例如:5★3=(5+3)×(5﹣3)=8×2=16,下面给出了关于这种新运算的几个结论:① 3★(﹣2)=5;②a★b=b★a;③若b=0,则a★b=a2;④若a★b=0,则a=b.其中正确结论的有__;(只填序号)
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有如图所示的一块地,已知AD=4米,CD=3米,![]() ,AB=13米,BC=12米.
,AB=13米,BC=12米.
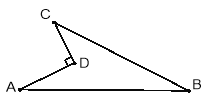
(1)试判断以点A、点B、点C为顶点的三角形是什么三角形?并说明理由.
(2)求这块地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司要同时运输A、B两种型号的商品共13件,A型商品每件体积为2m3 , 每件质量为1吨;B型商品每件体积为0.8m3 , 每件质量为0.5吨,这两种型号商品体积之和不超过18.8m3 , 质量之和大于8.5吨.
(1)求A、B两种型号商品的件数共有几种可能?写出所有可能情况;
(2)若一件A型商品运费为200元,一件B型商品运费为180元.则(1)中哪种情况的运费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
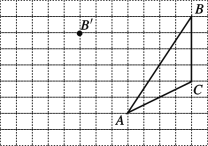
【题目】利用网格点和三角板画图或计算:
(1)在给定方格纸中画出平移后的![]() ;
;
(2)画出![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 边上的高线
边上的高线![]() ;
;
(4)![]() 的面积为_________;
的面积为_________;
(5)在图中能使![]() 的格点
的格点![]() 的个数有________个(点
的个数有________个(点![]() 异于点
异于点![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为4000元的电视以4400元售出,平均每天能售出6台.为了配合国家财政推出的“节能家电补贴政策”的实施,商场决定采取适当的降价措施,调查发现:这种电视的售价每降价50元,平均每天就能多售出3台.
(1)现设每台电视降价x元,商场每天销售这种电视的利润是y元,请写出y与x之间的函数表达式.(不要求写出自变量的取值范围)
(2)每台电视降价多少元时,商场每天销售这种电视的利润最高?最高利润是多少?
(3)商场要想在这种电视销售中每天盈利3600元,同时又要使百姓得到更多实惠,每台电视应降价多少元?根据以上的结论,请你直接写出售价在什么范围时,每个月的利润不低于3600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3![]() ﹣(+2
﹣(+2![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(﹣0.75);
)﹣(﹣0.75);
(2)(![]() ﹣
﹣![]() +
+![]() )×(﹣78);
)×(﹣78);
(3)(﹣![]() )÷(1
)÷(1![]() ﹣
﹣![]() ﹣
﹣![]() );
);
(4)﹣32﹣2÷![]() ×[2﹣(﹣
×[2﹣(﹣![]() )2]﹣(﹣2)3.
)2]﹣(﹣2)3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC的两边分别平行于∠DEF的两条边,且∠ABC=45°.
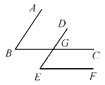
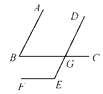
图1 图2
(1)图1中:∠DEF=_________,图2中:∠DEF=_________;
(2)请观察图1、图2中∠DEF分别与∠ABC有怎样的关系,请你归纳出一个命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元,若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com