
【题目】某物流公司要同时运输A、B两种型号的商品共13件,A型商品每件体积为2m3 , 每件质量为1吨;B型商品每件体积为0.8m3 , 每件质量为0.5吨,这两种型号商品体积之和不超过18.8m3 , 质量之和大于8.5吨.
(1)求A、B两种型号商品的件数共有几种可能?写出所有可能情况;
(2)若一件A型商品运费为200元,一件B型商品运费为180元.则(1)中哪种情况的运费最少?最少运费是多少?
【答案】
(1)
解:设A型商品x件,B型商品(13﹣x)件.
由题意可得: ![]() ,
,
解得:4<x≤7,
∴A、B两种型号商品的件数共有3种可能
所有可能情况为:A,5件,B,8件;A,6件,B,7件;A,7件,B,6件
(2)
解:∵一件A型商品运费为200元,一件B型商品运费为180元,
∴A商品越少则总运费越少,
∴当A,5件,B,8件时运费最低,最少运费是:200×5+8×180=2440(元)
【解析】(1)根据不等关系式为:2×A型商品件数+0.8×B型商品件数≤18.8,1×A型商品件数+0.5×B型商品件数>8.5,进而求出即可;(2)根据A型,B型商品运费得出A商品越少则总运费越少,进而求出即可.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为60cm的正方形硬纸片,剪掉阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使A、B、C、D四个点重合于图中的点P,正好形成一个底面是正方形的长方体包装盒.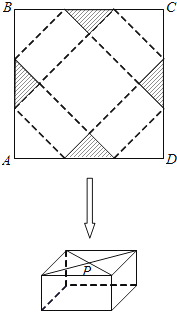
(1)若折叠后长方体底面正方形的面积为1250cm2 , 求长方体包装盒的高;
(2)设剪掉的等腰直角三角形的直角边长为x(cm),长方体的侧面积为S(cm2),求S与x的函数关系式,并求x为何值时,S的值最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
频数(通话次数) | 20 | 16 | 9 | 5 |
则5月份通话次数中,通话时间不超过15分钟的所占百分比是( )
A. 10% B. 40% C. 50% D. 90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据2013﹣2017年某市财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
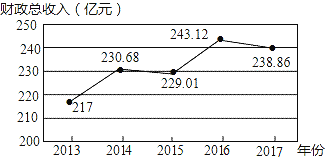
A. 2013~2017年财政总收入呈逐年增长
B. 预计2018年的财政总收入约为253.43亿元
C. 2014~2015年与2016~2017年的财政总收入下降率相同
D. 2013~2014年的财政总收入增长率约为6.3%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减轻学生的课业负担,某市教育行政部门规定中学生每天完成家庭作业的平均时间不能超过1.5小时,为了了解该市中学生课业负担情况,对部分学生每天完成家庭作业所用的时间进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)分别求出每天完成家庭作业所用的时间为“1小时”和“2小时”的学生人数占总人数的百分比,以及所用的时间为“1.5小时”的学生人数,并补全两个统计图;
(3)本次调查中,中学生每天完成家庭作业所用的平均时间是否符合要求?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有理数的原有运算法则中,我们补充定义一种新运算“★”如下:a★b=(a+b)(a﹣b),例如:5★3=(5+3)×(5﹣3)=8×2=16,下面给出了关于这种新运算的几个结论:① 3★(﹣2)=5;②a★b=b★a;③若b=0,则a★b=a2;④若a★b=0,则a=b.其中正确结论的有__;(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com