Question

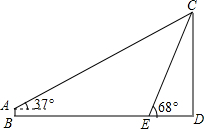
5．如图，条幅从楼顶C处拉下，在E处固定，条幅CE与地面成68°角，在离楼底D点40米处安置测角仪AB，在A处测得点C的仰角为37°．已知测角仪的高为1.5米，求条幅的长度（结果保留整数，参考数据：sin68°≈0.93，cos68°≈0.37，tan68°≈2.50，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

Answer 1

分析 由题意可先过点A作AH⊥CD于H．在Rt△ACH中，可求出CH，进而CD=CH+HD=CH+AB，再在Rt△CED中，求出CE的长．

解答 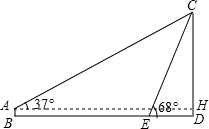解：过点A作AH⊥CD，垂足为H，
由题意可知四边形ABDH为矩形，∠CAH=37°，
则AB=DH=1.5米，BD=AH=40米，
∵在Rt△ACH中，tan∠CAH=$\frac{CH}{AH}$，
∴CH=AH•tan∠CAH，
∴CH=AH•tan∠CAH=40•tan37°≈40×0.75=30（米），
∵DH=1.5米，
∴CD≈30+1.5=31.5，
在Rt△CDE中，∵∠CED=60°，sin∠CED=$\frac{CD}{CE}$，
∴CE=$\frac{CD}{sin68°}$≈$\frac{31.5}{0.93}$≈34（米），
答：条幅的长约为34米．

点评 此题主要考查解直角三角形的应用-仰角俯角问题．要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．