
解:(1)∵|n|+

=0,
又|n|>0,

≥0,
∴m-1=0,
∴m=1,
∴A(1,0),
∴OA=1;
(2)答:AE的长度不变.
证明:∵△OAB是等边三角形,
∴BO=BA,∠OBA=60°,
又∵△BCD是等边三角形,
∴BC=BD,∠CBD=60°,
∴∠OBA=∠CBD=60°,
∴∠OBA-∠OBD=∠CBD-∠OBD,
∴∠ABD=∠OBC,
在△ABD和△OBC中,

,
可得△ABD≌△OBC(SAS),
∴∠ADB=∠OCB,又∠AFD=∠BFC,
可得∠DAO=∠DBC=60°,
∵EO⊥OA,即∠AOE=90°,
∴∠AEO=30°,
可得AE=2OA=2,
即当C点在x轴负半轴上运动时,AE的长度不变;
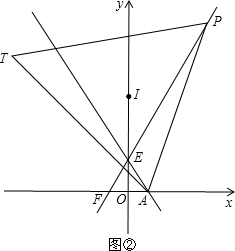
(3)答:点I总在y轴上运动.

证明:连接IA,IP,过I点作IM⊥AE,IN⊥FE,M,N分别为垂足.
易得△EFA为等边三角形,
∴∠MEN=∠FEA=60°,
∴∠MIN=120°
又∵IA,IP分别是∠TAP与∠TPA的角平分线,
可得∠AIP=120°,IA=IP
∴∠MIA=∠NIP
∴△MIA≌△NIP
∴IM=IN
∴点I在∠MEN的平分线上,
∵根据对顶角相等,∠MEI=∠OEA=∠NEI=∠OEF=30°,则y轴是∠MEN的平分线所在的直线
∴当点P运动时,点I总在y轴上运动.
分析:(1)根据被开方数不为负数,可知m-1=0,由此可得出m=1,那么A的坐标应该是A(1,0),由此即可求出OA的长度;
(2)要看AE是否会改变,只需看∠DAO的度数是否会改变,由于BC=DB,BA=OB,∠OBC=∠ABD=60°-∠OBD,因此△BOC和△BAD就全等,那么可得出∠DAB=∠BOC=120°,即∠OAD=60°,因此AE的长是不会变化的,且AE=2OA=2,由此即可解决问题;
(3)由于F,A关于y轴对称,那么y轴应该是∠FEA和它的对顶角的平分线,那么要看I是否在y轴上,只需看看I到AE,EF的距离是否相等即可,可过I分别作这两条直线的垂线设为IM,IN,那么关键是证IM=IN,可通过构建全等三角形来证明,连接PI,AI.那么关键是证三角形AIM和PIN全等,已知的有一组直角,PI=AI,只需再得出一组对应角相等即可,由于三角形EAF是等边三角形,因此∠MEN=60°,∠MIN=120°,而PI,AI都是角平分线且平分的都是60°的角,因此∠PIA=120°,那么这两个120°角都减去∠AIN后可得出∠MIA=∠PIN,由此可得出两三角形全等,那么IM=IN,因此I总在y轴上运动.
点评:本题主要考查了等边三角形的性质,全等三角形的判定等知识点,根据全等三角形得出边和角相等是解题的关键.

 =0.以OA为一边,在第四象限内作等边△OAB.C是x轴负半轴上的一动点,连接CB,在CB的上方作等边△DCB,直线DA交y轴于E点.
=0.以OA为一边,在第四象限内作等边△OAB.C是x轴负半轴上的一动点,连接CB,在CB的上方作等边△DCB,直线DA交y轴于E点.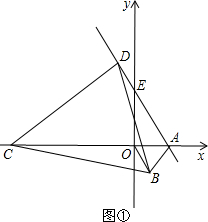
 解:(1)∵|n|+
解:(1)∵|n|+ =0,
=0, ≥0,
≥0, ,
,


 快捷英语周周练系列答案
快捷英语周周练系列答案 (2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,cos∠AOB=
(2013•松江区模拟)已知:点A、B都在半径为9的圆O上,P是射线OA上一点,以PB为半径的圆P与圆O相交的另一个交点为C,直线OB与圆P相交的另一个交点为D,cos∠AOB=

