
【题目】命题“直径所对的圆周角是直角”的逆命题是 .
科目:初中数学 来源: 题型:
【题目】通信市场竞争日益激烈,某通信公司的手机市话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答 
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D.
(2)阅读下面的内容,并解决后面的问题: 如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数.
解:∵AP、CP分别平分∠BAD、∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P= ![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
①如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.
②在图4中,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
③在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论,无需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成证明,说明理由. 已知:如图,点D在BC边上,DE、AB交于点F,AC∥DE,∠1=∠2,∠3=∠4.
求证:AE∥BC.
证明:∵AC∥DE(已知),
∴∠4=()
∵∠3=∠4(已知),
∴∠3=()
∵∠1=∠2(已知),
∴∠1+∠FAD=∠2+∠FAD()
即∠FAC=∠EAD,
∴∠3= .
∴AE∥BC()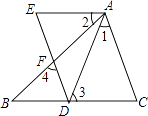
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)计算:2(x+y)(x﹣y)﹣(x+y)2;
(2)解方程: ![]() ;
;
(3)先化简,再求值:v,在0,1,2三个数中选一个合适的数并代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于点C(0,5).
(1)求该抛物线所对应的函数关系式;
(2)D是笫一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD.设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围;
②当m为何值时,S有最大值,并求这个最大值;
③直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com