
【题目】解答
(1)计算:2(x+y)(x﹣y)﹣(x+y)2;
(2)解方程: ![]() ;
;
(3)先化简,再求值:v,在0,1,2三个数中选一个合适的数并代入求值.
【答案】
(1)解:原式=2x2﹣2y2﹣(x2+2xy+y2)
=2x2﹣2y2﹣x2﹣2xy﹣y2
=x2﹣3y2﹣2xy
(2)解:去分母得x+x﹣2=4,
解得x=3,
检验:x=3时,x﹣2≠0,则x=2是原方程的解,
所以原方程的解为x=3
(3)解:原式= ![]()
![]() +
+ ![]()
= ![]() +
+ ![]()
= ![]() ,
,
当x=1时,原式= ![]() =0
=0
【解析】(1)先利用平方差公式和完全平方公式展开,然后合并即可;(2)方程两边同乘以x﹣2得到整式方程,解得x=3,然后进行检验确定原方程的解;(3)先把分子分母因式分解,再把除法运算化为乘法运算,然后约分后合并得到原式= ![]() ,由于x=0或x=2时,原分式无意义,则把x=0代入计算即可.
,由于x=0或x=2时,原分式无意义,则把x=0代入计算即可.
【考点精析】关于本题考查的去分母法,需要了解先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x﹣y)2=0.
(1)求B点坐标;
(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC. 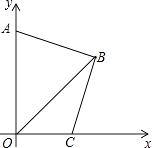
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,∠BAC=90°,CD=![]() BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
(1)如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长;
(2)如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证MN⊥AE;
(3)如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索![]() 的值并直接写出结果
的值并直接写出结果
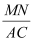
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件进价为100元的商品,先按进价提高20%作为标价,但因销量不好,又决定按标价降价20%出售。那么这次生意的盈亏情况是每件( )
A. 不亏不赚 B. 亏了4元 C. 赚了4元 D. 赚了6元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com