
����Ŀ����֪��ABC�ǵ��������Σ���BAC=90����CD=![]() BC��DE��CE��DE=CE������AE����M��AE���е�.
BC��DE��CE��DE=CE������AE����M��AE���е�.
��1����ͼ1������D��BC���ϣ�����CM����AB=4ʱ����CM�ij���
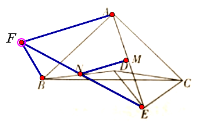
��2����ͼ2������D����ABC���ڲ�������BD����N��BD�е㣬����MN��NE����֤MN��AE��
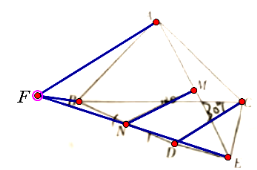
��3����ͼ3����ͼ2�е���CDE�Ƶ�C��ʱ����ת��ʹ��BCD=30��������BD����N��BD�е㣬����MN��̽��![]() ��ֵ��ֱ��д�����
��ֵ��ֱ��д�����
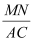
���𰸡���1��![]() ����2��֤�����̼���������3��
����2��֤�����̼���������3��![]() .
.
��������
�����������1�����ݵ���ֱ��������ABC�ó�BC�ij��ȣ�Ȼ����ݵ���ֱ��������DCE�ó�CE�ij��ȣ�Ȼ�����Rt��ACE�Ĺ��ɶ����ó�AE�ij��ȣ��Ӷ�����ֱ��������б���ϵ����ߵ���б�ߵ�һ��ó��𰸣���2���ӳ�EN��NF��ʹNE=NF��������BF��AF��Ȼ��֤����ABF�ա�ACE���Ӷ��ó���FAE=��BAC=90����Ȼ�����ƽ���ߵ����ʵó��𰸣���3�����ݵڶ���ͬ���ķ����ó�MN=![]() AF��AF=AE���Ӷ��ó���.
AF��AF=AE���Ӷ��ó���.
�����������1����AB=AC=4 ��BAC=90�� ��BC=4![]() ��CD=2
��CD=2![]() ��CE=2��
��CE=2��
����Rt��ACE�Ĺ��ɶ����ɵã�AE=![]() ��CM=
��CM=![]()
��2����ͼ���ӳ�EN��NF��ʹNE=NF��������BF��AF��
�ɵ�BF=DE=CE����FBN=��NDE�� ����ACE=90��-��DCB
��ABF=��BDE-��ABN=��180��-��DBC-��DCB-��EDC-��ABN=180��-����DBC+��ABN��-45��-��DCB=90��-��DCB
������ACE=��ABF��������ABF�ա�ACE�� ������FAB=��EAC�� ������FAE=��BAC=90����
��ΪMN//AF������MN��AE��
��3��ͬ��2���ɵ�MN=![]() AF��AF=AE��
AF��AF=AE��
��AC=2CE����ACE=120���������AE=![]() �� ����
�� ����![]()


 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˵�����٩�a��ʾ�������ھ���ֵ��С����������0����3��102x2y��5�ε���ʽ���� ![]() �Ƕ���ʽ��������ȷ���ǣ� ��
�Ƕ���ʽ��������ȷ���ǣ� ��
A.�٢�
B.�ڢ�
C.�ڢ�
D.�٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��Ӧ�������˸��������ĺ��٣��ı�ˮ����ʧ������״��2016��ij�����˸�����1200Ķ���ƻ�2018���˸�����1728Ķ.��������ƽ��ÿ���˸����ֵ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����֤����˵�����ɣ� ��֪����ͼ����D��BC���ϣ�DE��AB���ڵ�F��AC��DE����1=��2����3=��4��
��֤��AE��BC��
֤������AC��DE����֪����
���4=����
�ߡ�3=��4����֪����
���3=����
�ߡ�1=��2����֪����
���1+��FAD=��2+��FAD����
����FAC=��EAD��
���3= ��
��AE��BC����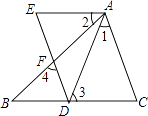
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������B=40�㣬A��C�ֱ�Ϊ�������ϵ�����һ�㣬����AC����BAC���ACB��ƽ���߽��ڵ�P1 �� ���P1= �� D��FҲΪ�������ϵ�����һ�㣬����DF����BFD���FDB��ƽ���߽��ڵ�P2 �� �����������ɣ����P2016= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����
��1�����㣺2��x+y����x��y������x+y��2��
��2���ⷽ�̣� ![]() ��
��
��3���Ȼ�������ֵ��v����0��1��2��������ѡһ�����ʵ�����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij����ð������ֱ��ԼΪ0.000000823�ף���0.000000823�ÿ�ѧ��������ʾΪ��������
A. 8.23��10��6 B. 8.23��10��7 C. 8.23��106 D. 8.23��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ�κ�����ͼ���㣨-1��2�����Ҿ�����һ�����������ޣ�����д��һ���������������ĺ�����ϵʽ_____________________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com