
【题目】在平面直角坐标系中,B点坐标为(x、y),且x、y满足|x+y﹣8|+(x﹣y)2=0.
(1)求B点坐标;
(2)如图,点A为y轴正半轴上一点,过点B作BC⊥AB,交x轴正半轴于点C,求证:AB=BC. 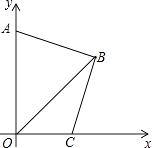
【答案】
(1)解:∵|x+y﹣8|+(x﹣y)2=0,
∴ ![]() ,
,
解得, ![]() ,
,
即点B的坐标为(4,4)
(2)解:作BD⊥OA于点D,作BE⊥OC于点E,如右图所示,
∵BC⊥AB,∠DBE=90°,∠ADB=∠CEB=90°,
∴∠ABC=90°,
∴∠ABD+∠DBC=∠DBC+∠CBE=90°,
∴∠ABD=∠CBE,
又∵点B(4,4),
∴BD=BE=4,
∴△ADB≌△CEB(ASA),
∴AB=BC.
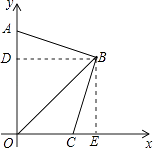
【解析】(1)根据x、y满足|x+y﹣8|+(x﹣y)2=0,可以求得x、y的值,从而可以求得点B的坐标;(2)根据题意,可以作辅助线,只要证明△ADB≌△CEB即可证明AB与BC的关系,根据题目中的条件可以得到△ADB≌△CEB的条件,本题得以解决.
【考点精析】掌握解二元一次方程组是解答本题的根本,需要知道二元一次方程组:①代入消元法;②加减消元法.


科目:初中数学 来源: 题型:
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B, 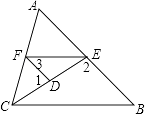
(1)求证:∠AFE=∠ACB;
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通信市场竞争日益激烈,某通信公司的手机市话费标准按原标准每分钟降低a元后,再次下调了20%,现在收费标准是每分钟b元,则原收费标准每分钟是元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有五种说法:①﹣a表示负数;②绝对值最小的有理数是0;③3×102x2y是5次单项式;④ ![]() 是多项式.其中正确的是( )
是多项式.其中正确的是( )
A.①③
B.②④
C.②③
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简); 
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
证明:DE=BD+CE.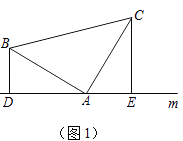
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由. 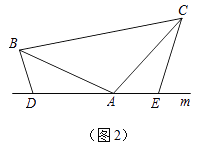
(3)拓展与应用:如图(3),D,E是D,A,E三点所在直线m上的两动点(D,A, E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状. 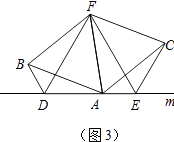
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答
(1)计算:2(x+y)(x﹣y)﹣(x+y)2;
(2)解方程: ![]() ;
;
(3)先化简,再求值:v,在0,1,2三个数中选一个合适的数并代入求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com