Question

16．两个反比例函数和在第一象限内的图象如图所示，点P在的图象上，PC⊥x轴于点C，交的图象于点A，PD⊥轴于点D，交的图象于点B，当点P在的图象上运动时，下列结论错误的是（　　）

• A． △ODB与△OCA的面积相等
• B． 当点A是PC的中点时，点B一定是PD的中点
• C． 只有当四边形OCPD为正方形时，四边形PAOB的面积最大
• D． $\frac{CA}{PA}$=$\frac{DB}{PB}$

Answer 1

分析 根据反比例函数的图象和性质，特别是根据反比例函数k的几何意义，对四个选项逐一进行分析，即可得出正确答案．

解答 解：A、由于点A和点D均在同一个反比例函数y=$\frac{1}{x}$的图象上，所以S_△ODB=$\frac{1}{2}$，S_△OCA=$\frac{1}{2}$；故△ODB与△OCA的面积相等，故本选项正确；
B、连接OP，点A是PC的中点，
则△OAP和△OAC的面积相等，
∵△ODP的面积=△OCP的面积=$\frac{k}{2}$，△ODB与△OCA的面积相等，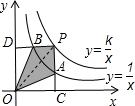
∴△OBP与△OAP的面积相等，
∴△OBD和△OBP面积相等，
∴点B一定是PD的中点，故本选项正确；
C、由于矩形OCPD、三角形ODB、三角形OCA为定值，则四边形PAOB的面积不会发生变化，故本选项错误；
D、设P（m，$\frac{k}{m}$），则A（m，$\frac{1}{m}$），B（$\frac{m}{k}$，$\frac{k}{m}$），则CA=$\frac{1}{m}$，PA=$\frac{k}{m}$-$\frac{1}{m}$，DB=$\frac{m}{k}$，PB=m-$\frac{m}{k}$，
故$\frac{CA}{PA}$=$\frac{\frac{1}{m}}{\frac{k}{m}-\frac{1}{m}}$=$\frac{1}{k-1}$，$\frac{DB}{PB}$=$\frac{\frac{m}{k}}{m-\frac{m}{k}}$=$\frac{1}{k-1}$，所以$\frac{CA}{PA}$=$\frac{DB}{PB}$，故D正确．
故选C．

点评 本题考查了反比例函数的综合题，关键是设P点坐标，利用点与点的坐标关系，反比例函数的性质表示相关线段的长，对每一个结论进行判断．