
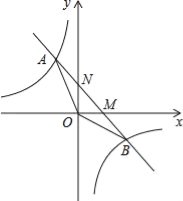
【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数![]() 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.
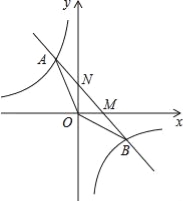
【答案】(1)y1=﹣x+2,(2)6;(3)x<﹣2或0<x<4
【解析】
试题分析:(1)先根据反比例函数解析式求得两个交点坐标,再根据待定系数法求得一次函数解析式;
(2)将两条坐标轴作为△AOB的分割线,求得△AOB的面积;
(3)根据两个函数图象交点的坐标,写出一次函数图象在反比例函数图象上方时所有点的横坐标的集合即可.
试题解析:(1)设点A坐标为(﹣2,m),点B坐标为(n,﹣2)
∵一次函数y1=kx+b(k≠0)的图象与反比例函数y2=﹣![]() 的图象交于A、B两点
的图象交于A、B两点
∴将A(﹣2,m)B(n,﹣2)代入反比例函数y2=﹣![]() 可得,m=4,n=4
可得,m=4,n=4
∴将A(﹣2,4)、B(4,﹣2)代入一次函数y1=kx+b,可得
![]() ,解得
,解得![]()
∴一次函数的解析式为y1=﹣x+2;,
(2)在一次函数y1=﹣x+2中,
当x=0时,y=2,即N(0,2);当y=0时,x=2,即M(2,0)
∴![]() =
=![]() ×2×2+
×2×2+![]() ×2×2+
×2×2+![]() ×2×2=2+2+2=6;
×2×2=2+2+2=6;
(3)根据图象可得,当y1>y2时,x的取值范围为:x<﹣2或0<x<4


科目:初中数学 来源: 题型:
【题目】甲、乙两组工人同时加工某种零件,乙组在工作中有一次停产更换设备,之后乙组的工作效率是原来的1.2倍,甲、乙两组加工出的零件合在一起装箱,每200件装一箱,零件装箱的时间忽略不计,两组各自加工零件的数量y(件)与时间x(时)的函数图象如图,以下说法错误的是( )
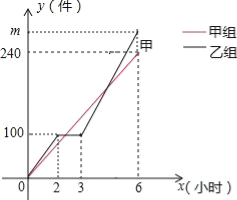
A.甲组加工零件数量y与时间x的关系式为y甲=40x
B.乙组加工零件总量m=280
C.经过![]() 小时恰好装满第1箱
小时恰好装满第1箱
D.经过![]() 小时恰好装满第2箱
小时恰好装满第2箱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盈盈超市第一次用6000元购进甲,乙两种商品,其中乙商品的件数比甲商品件数的 ![]() 多15件,甲,乙两种商品的进价和零售价如下表(注:获利=售价﹣进价):
多15件,甲,乙两种商品的进价和零售价如下表(注:获利=售价﹣进价):
甲 | 乙 | |
进价(件/元) | 22 | 30 |
售价(件/元) | 29 | 40 |
(1)第一次进货时甲,乙两种商品各购进多少件?
(2)该超市第二次以第一次的进价又购进甲,乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍,甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完后盈利2130元,求第二次乙种商品是按原价打几折销售的.
查看答案和解析>>
科目:初中数学 来源: 题型:
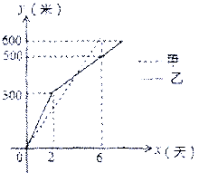
【题目】据悉,沙坪坝火车站改造工程预计于2015年完工并投入使用,到时可有效解决三峡广场堵车问题。现有甲、乙两工程队分别同时修建两条600米长的道路,己知修建道路长度![]() (米)与修建时间
(米)与修建时间![]() (天)之间的关系如图所示,则下列说法中错误的是( )
(天)之间的关系如图所示,则下列说法中错误的是( )
A.甲队每天修建100米;
B. 第6天,甲队比乙队多修建100米;
C.乙队开工两天后,每天修建50米;
D. 甲队比乙队提前3天完成任务.
查看答案和解析>>
科目:初中数学 来源: 题型:
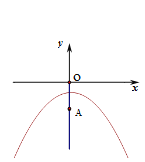
【题目】已知抛物线![]()
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点 N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com