
【题目】在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为![]() 、
、![]() (km),
(km),![]() 、
、![]() 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A.C两港口间的距离为 km, ![]() ;
;
(2)求图中点P的坐标;
(3)何时甲、乙两船相距18km.

【答案】(1)120, 2;(2)(1,30);(3)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)从图中可以看出A、B两港是30km,B、C两港是90km,A、C两港口间的距离为30+90=120km,求出甲的速度,进而求出a的值;
(2)求出y1=60x﹣30,y2=30x,解出两个函数的交点,就是点P的坐标.
(3)先根据一次函数的图象求出甲及乙的速度,再根据甲在乙船前和乙船后,及甲船已经到了而乙船正在行驶,三种情况进行解答即可.
试题解析:解:(1)从图中可以看出A、B两港是30km,B、C两港是90km,∴A、C两港口间的距离为30+90=120km,甲的速度为:30÷0.5=60,a=120÷60=2.故答案为:120,2.
(2)由点(3,90)求得,y2=30x,当x≥0.5时,由点(0.5,0),(2,90)求得,y1=60x﹣30,当y1=y2时,60x﹣30=30x,解得x=1,此时y1=y2=30,∴点P的坐标是(1,30).
(3)甲的速度为每小时60千米,乙的速度为每小时30千米,设x小时相距18千米,分三种情况讨论:
①第一种情况:60x﹣30x=30﹣18,解得x=![]() ;
;
②第二种情况:60x﹣30x=30+18,解得,x=![]() ;
;
③第三种情况,甲船停靠C港后,乙船继续航行,当乙船行72千米时,与甲船也相距18千米,所以时间为:72÷30=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列各式计算正确的是( )
A.(x+y)2=x2+y2B.(x+3)(x﹣3)=x2﹣3
C.(m﹣n)(n﹣m)=n2﹣m2D.(x﹣y)2=(y﹣x)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备组织部分学生到少年宫参加活动,陈老师从少年宫带回来两条信息:
信息一:按原来报名参加的人数,共需要交费用320元,如果参加的人数能够增加到原来人数的2倍,就可以享受优惠,此时只需交费用480元;
信息二:如果能享受优惠,那么参加活动的每位同学平均分摊的费用比原来少4元.
根据以上信息,原来报名参加的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
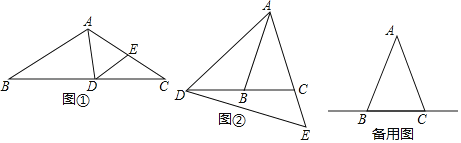
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com