
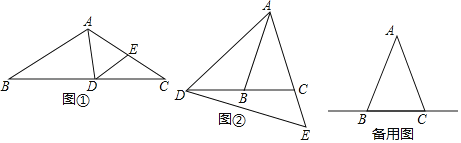
【题目】如图,△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且AD=AE,连接DE.
⑴如图①,若∠B=∠C=35°,∠BAD=80°,求∠CDE的度数;
⑵如图②,若∠ABC=∠ACB=75°,∠CDE=18°,求∠BAD的度数;
⑶当点D在直线BC上(不与点B、C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
【答案】(1)40°;(2)36°;(3)∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.
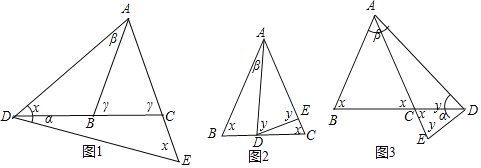
【解析】试题分析:(1)根据等腰三角形的性质得到∠BAC=110°,根据等腰三角形的性质和三角形的外角的性质即可得到结论; (2)根据三角形的外角的性质得到∠E=75°-18°=57°,根据等腰三角形的性质和三角形的外角的性质即可得到结论; (3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β,分3种情况:①如图1,当点D在点B的左侧时,∠ADC=x°-α,②如图2,当点D在线段BC上时,∠ADC=y°+α,③如图3,当点D在点C右侧时,∠ADC=y°-α,根据这3种情况分别列方程组即,解方程组即可得到结论.
试题解析:
(1)∵∠B=∠C=35°,
∴∠BAC=110° ,
∵∠BAD=80°,
∴∠DAE=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠CDE=∠AED-∠C=75°35°=40°;
(2)∵∠ACB=75°,∠CDE=18° ,
∴∠E=75°18°=57°,
∴∠ADE=∠AED=57°,
∴∠ADC=39°,
∵∠ABC=∠ADB+∠DAB=75° ,
∴∠BAD=36°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β
①如图1,当点D在点B的左侧时,∠ADC=x°﹣α
∴![]() ,(1)﹣(2)得,2α﹣β=0,
,(1)﹣(2)得,2α﹣β=0,
∴2α=β;
②如图2,当点D在线段BC上时,∠ADC=y°+α
∴![]() ,(2)﹣(1)得,α=β﹣α,
,(2)﹣(1)得,α=β﹣α,
∴2α=β;
③如图3,当点D在点C右侧时,∠ADC=y°﹣α
∴![]() ,(2)﹣(1)得,2α﹣β=0,
,(2)﹣(1)得,2α﹣β=0,
∴2α=β.
综上所述,∠BAD与∠CDE的数量关系是2∠CDE=∠BAD.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为![]() 、
、![]() (km),
(km),![]() 、
、![]() 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A.C两港口间的距离为 km, ![]() ;
;
(2)求图中点P的坐标;
(3)何时甲、乙两船相距18km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定理中,没有逆定理的是( )
A. 同旁内角互补,两直线平行
B. 直角三角形的两锐角互余
C. 互为相反数的两个数的绝对值相等
D. 同位角相等,两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组线段的长为边,能组成三角形的是( )
A.2cm,3cm,4cm
B.2cm,3cm,5cm
C.2cm,5cm,10cm
D.8cm,4cm,4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把(+5)﹣(+3)﹣(﹣1)+(﹣4)写成省略括号的和的形式是( )
A.﹣5﹣3+1﹣4
B.5﹣3﹣1﹣4
C.5﹣3+1﹣4
D.5+3+1﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列与:﹣9+31+28﹣45相等的是( )
A.﹣9+45+28﹣31
B.31﹣45﹣9+28
C.28﹣9﹣31﹣45
D.45﹣9﹣28+31
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com