
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OC,根据切线的性质和已知求出OC∥AD,求出∠OCA=∠CAO=∠DAC,即可得出答案;
(2)连接BE、BC、OC,BE交AC于F交OC于H,根据cos∠CAD=![]() =
=![]() ,设AD=4a,AC=5a,则DC=EH=HB=3a,根据cos∠CAB=
,设AD=4a,AC=5a,则DC=EH=HB=3a,根据cos∠CAB=![]() =
=![]() ,求出AB、BC,再根据勾股定理求出CH,由此即可解决问题;
,求出AB、BC,再根据勾股定理求出CH,由此即可解决问题;
试题解析:解:(1)连接OC,∵CD是⊙O的切线,∴CD⊥OC,又∵CD⊥AD,∴AD∥OC,∴∠CAD=∠ACO,∵OA=OC,∴∠CAO=∠ACO,∴∠CAD=∠CAO,即AC平分∠DAB;

(2)连接BE、BC、OC,BE交AC于F交OC于H.∵AB是直径,∴∠AEB =90°,∴∠AEB=∠DEH=∠D=∠DCH=90°,∴四边形DEHC是矩形,∴∠EHC=90°,即OC⊥EB,∴DC=EH=HB,DE=HC,∵cos∠CAD=![]() =
=![]() ,设AD=4a,AC=5a,则DC=EH=HB=3a,∵cos∠CAB=
,设AD=4a,AC=5a,则DC=EH=HB=3a,∵cos∠CAB=![]() =
=![]() ,∴AB=
,∴AB=![]() a,BC=
a,BC=![]() a,在RT△CHB中,CH=
a,在RT△CHB中,CH=![]() =
=![]() a,∴DE=CH=
a,∴DE=CH=![]() a,AE=
a,AE=![]() =
=![]() a,∵EF∥CD,∴
a,∵EF∥CD,∴![]() =
=![]() =
=![]() .
.



 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
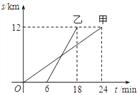
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y=kx(k≠0)的图象经过点(2,﹣1),则这个函数的图象必经过点( )
A. (﹣1,2)B. (1,2)C. (2,1)D. (﹣2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=![]() 的图象的两个交点;
的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了“学生使用手机调研”活动,随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,图②的统计图.已知“查资料”的人数是40人.

(1)在这次调查中,一共抽取了 名学生;
(2)在扇形统计图中,“玩游戏”对应的圆心角的度数是 度;
(3)补全条形统计图;(注:0-1小时有16人)
(4)该校共有学生2660人,请估计每周使用手机时间在2小时以上(不含2小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某个“清凉小屋”自动售货机出售![]() 三种饮料.
三种饮料.![]() 三种饮料的单价分别是2元/瓶、3元/瓶、5元/瓶. 工作日期间,每天上货量是固定的,且能全部售出,其中,
三种饮料的单价分别是2元/瓶、3元/瓶、5元/瓶. 工作日期间,每天上货量是固定的,且能全部售出,其中,![]() 饮料的数量(单位:瓶)是
饮料的数量(单位:瓶)是![]() 饮料数量的2倍,
饮料数量的2倍,![]() 饮料的数量(单位:瓶)是
饮料的数量(单位:瓶)是![]() 饮料数量的2倍. 某个周六,
饮料数量的2倍. 某个周六,![]() 三种饮料的上货量分别比一个工作日的上货量增加了50%,60%,50%,且全部售出. 但是由于软件bug,发生了一起错单(即消费者按某种饮料1瓶的价格投币,但是取得了另一种饮料1瓶),结果这个周六的销售收入比一个工作日的销售收入多了403元. 则这个“清凉小屋”自动售货机一个工作日的销售收入是__________元.
三种饮料的上货量分别比一个工作日的上货量增加了50%,60%,50%,且全部售出. 但是由于软件bug,发生了一起错单(即消费者按某种饮料1瓶的价格投币,但是取得了另一种饮料1瓶),结果这个周六的销售收入比一个工作日的销售收入多了403元. 则这个“清凉小屋”自动售货机一个工作日的销售收入是__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与x轴交于点C与直线AD交于点A(1,2),点D的坐标为(0,1)
(1)求直线AD的解析式;
(2)直线AD与x轴交于点B,请判断△ABC的形状;
(3)在直线AD上是否存在一点E,使得4S△BOD=S△ACE,若存在求出点E的坐标,若不存在说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) -20+(-18)-12 +10
(2)![]()
(3) ![]()
(4)(-81)÷2![]() ×(-
×(-![]() )÷(-16)
)÷(-16)
(5) (-36) ÷4-5×(-1.2)
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
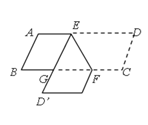
【题目】如图,在□ABCD中,点E,F分别在边AD、BC上,EF=2,∠DEF=60°将四边形EFCD沿EF翻折,得到四边形EFC’D’,ED’交BC于点G,则△GEF的周长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com