Question

【题目】如图，一次函数y=kx+3的图象分别交x轴、y轴于点B、点C，与反比例函数y= 的图象在第四象限的相交于点P，并且PA⊥y轴于点A，已知A （0，﹣6），且S△CAP=18．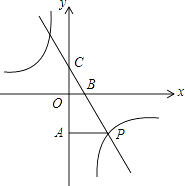
（1）求上述一次函数与反比例函数的表达式；
（2）设Q是一次函数y=kx+3图象上的一点，且满足△OCQ的面积是△BCO面积的2倍，求出点Q的坐标．

Answer 1

【答案】
（1）解：令一次函数y=kx+3中的x=0，则y=3，

即点C的坐标为（0，3），

∴AC=3﹣（﹣6）=9．

∵S△CAP= ACAP=18，

∴AP=4，

∵点A的坐标为（0，﹣6），

∴点P的坐标为（4，﹣6）．

∵点P在一次函数y=kx+3的图象上，

∴﹣6=4k+3，解得：k=﹣ ；

∵点P在反比例函数y= 的图象上，

∴﹣6= ，解得：n=﹣24．

∴一次函数的表达式为y=﹣ x+3，反比例函数的表达式为y=﹣

（2）解：令一次函数y=﹣ x+3中的y=0，则0=﹣ x+3，

解得：x= ，

即点B的坐标为（ ，0）．

设点Q的坐标为（m，﹣ m+3）．

∵△OCQ的面积是△BCO面积的2倍，

∴|m|=2× ，解得：m=± ，

∴点Q的坐标为（﹣ ，9）或（ ，﹣3）

【解析】（1）由一次函数表达式可得出点C的坐标，结合A点坐标以及三角形的面积公式可得出AP的长度，从而得出点P的坐标，由点P的坐标结合待定系数法即可求出一次函数及反比例函数的表达式；（2）设点Q的坐标为（m，﹣ m+3）．由一次函数的表达式可找出点B的坐标，结合等底三角形面积的性质可得出关于m的一元一次方程，解方程即可得出m的值，将其代入点Q的坐标中即可．